

光在光电实验中非常重要,对光的特性进行了解是有必要的。涉及到使用光源,我们要考虑到使用激光还是普通光源,若选择激光,那么波长应该选择多少,功率选择多大,所选择的激光器是那种类型的,对激光的稳定性是否有要求等等,当然还有很多其它要考虑的因素,在此不再赘述。本文主要通过描述麦克斯韦电磁波理论来简单介绍光的基本性质,例如麦克斯韦方程、波动方程、能量流、坡印廷矢量等。
展示全部 
光的传播
1.麦克斯韦方程组
光是一种电磁波,麦克斯韦方程的特性可以用四个方程来描述。
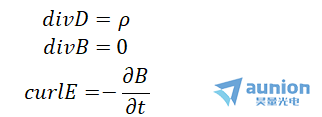

上式,E和H分别为电场和磁场矢量;p为自由电荷密度;J为自由电流密度;矢量场D和B分别为电位移和磁感应强度。
方程1是自由空间电场的高斯定理:通过一个封闭曲面的电通量正比于封闭曲面内的净电荷量。方程2是自由空间磁场的高斯定理:通过封闭曲面的磁通量为零。方程3是自由空间的法拉第感应定理的数学表达式:随时间变化的磁场产生电场。方程4是自由空间的安培定理,指出随时间变化的电场产生磁场。这4个方程在时间变化的情况下是相互影响的,电场和磁场相互作用构成电磁波,电场和磁场是由电荷和电流产生的。
洛伦兹定理指出,当电荷q在电磁场(E,B)中以一定的速度运动时,会受到力的作用,表达式如下:
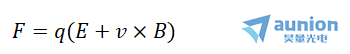
在电场和磁场的影响下物质的特性用物质方程来描述,物质方程在非色散、各向同性、连续介质的情况下,可表示为:

式中,Jc为传导电流密度;Xe和Xm分别为电化率和磁化率;介电常数ε和磁导率μ分别描述了均匀物质对给定频率的电学元件和磁性元件的反应。
在没有自由电荷(p=0)、非磁性、不导电(J=0,σ=0)的材料中:

在这里一个矢量的散度和旋度,例如矢量E的散度和旋度是:
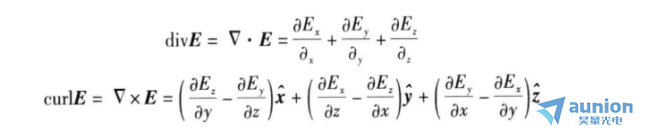
2.光的本质
自由空间的四个麦克斯韦方程联立起来,可以得到zui终的两个关于电场和磁场矢量的方程:

其中,拉普拉斯算子作用于E和B的每一个分量;因此,电磁场的每一个分量遵从标量波方程。这表明了以矢量形式在自由空间传播的电磁谐波的存在。即光的本质是电磁波。
(1)光是一种三维平面电磁波
由上式可知E和B的每一个分量都满足微分波动方程,这个事实可以说明光的三维平面电磁波性质。在一个垂直于传播矢量k的平面上的一点r变化的磁场和电场可用下面方程描述:

上式描述了具有相同频率和具有相同传播矢量k沿任意方向传播的电磁谐波。
(2)光是一种横波
电磁波是横波,因为矢量E和B位于垂直于传播方向的平面内,这个传播方向由k来决定。将上式代入麦克斯韦方程可得:

由于k·E=0,k·B=0,所以E和B一定垂直于k,这表明电磁波是横波。
3.能量流和坡印廷矢量
电磁波传播时携带能量。光波能量的表达式可以通过与电容和电感储存能量类比而得到:

光波的总能量密度是构成光波的电场和磁场的能量密度总和:

一个行波携带能量,能量以电磁场定义的电磁波功率形式进行传输。在一个时间间隔△t内,通过垂直于波的传输方向的面积为A的总能量为u△V。这里△V是由穿过的面积A和长度c△t决定的体积,c△t是波在时间间隔△t内所走过的距离。所以,波的功率可以表示为:
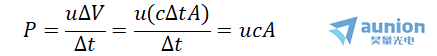
单位面积的功率或者说单位面积单位时间的能量流,为能量通量:

由于能量流沿着波的传输方向,能量通量S其实是一个矢量,E×B的方向就是能量流的方向,矢量S可由电场和磁场矢量表示成:

S即为坡印廷矢量。
了解更多详情,请访问上海昊量光电的官方网页:
https://www.auniontech.com/details-184.html
更多详情请联系昊量光电/欢迎直接联系昊量光电
关于昊量光电:
上海昊量光电设备有限公司是光电产品专业代理商,产品包括各类激光器、光电调制器、光学测量设备、光学元件等,涉及应用涵盖了材料加工、光通讯、生物医疗、科学研究、国防、量子光学、生物显微、物联传感、激光制造等;可为客户提供完整的设备安装,培训,硬件开发,软件开发,系统集成等服务。
您可以通过我们昊量光电的官方网站www.auniontech.com了解更多的产品信息,或直接来电咨询4006-888-532。