

光既有粒子性也有波动性,光具有波粒二象性。光的粒子性表现,比如光电发射效应,光的波动性表现,比如干涉和衍射。衍射是光波所固有的基本属性,利用激光光源所发出的相干光束可以很容易观察到衍射现象。与干涉类似,利用衍射花样的改变也可以测量位移或轮廓。本文将从夫琅禾费衍射来介绍衍射的基本特性,介绍一些衍射的相关公式。
衍射
1衍射的基本原理
如图1所示,考虑点光源Po发出的球面波(波长为λ,幅值为Up,),照明某孔径无限大不透明屏上孔径,我们来计算孔径右边空间某点P处的场值。包含P点的某闭合面由图1中的S1、S2和S3组成。其中,S2由于不透明,故对P点的场值没有贡献,半球区域S3,当满足索末菲辐射条件时就可以不考虑其对P点的贡献。这样,透光孔S1,决定了P点出的光波幅值Up。

图1 衍射推导
菲涅耳-基尔霍夫衍射公式:
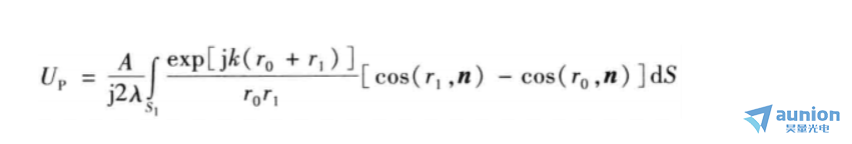
式中,(r1,n)为单位矢量r1和n之间的夹角,(ro,n)为ro和n之间的夹角。倾斜因子[cos(r1,n)-cos(ro,n)].
如果点光源离开孔径足够远,对于孔径上各点都有cos(r1,n)=1。另外设cos(ro,n)=-cosx,则可得:
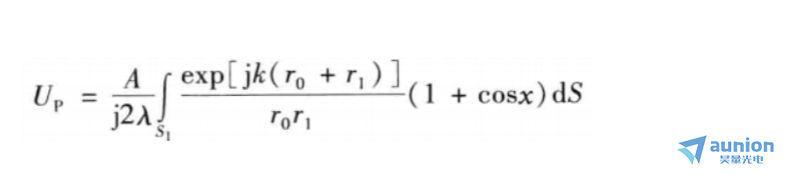
当P点远离衍射屏时,x近似等于零,倾斜因子近似等于2,所以上式可改写:

这样,关于空间某点P处的场值Up就可以极大的简化得出。
图2中,包含坐标原点O的孔径被单色平面波照射。这里,利用g(xo,yo)来描述孔径内某点的光源因素,并且其在观察屏上产生衍射花样。P。(xo,yo,0)是孔径平面上的一点,点P(x1,y1,z)位于观察屏上。r表示POP点之间的距离,P处的衍射分布记为U(x1,y1),则:
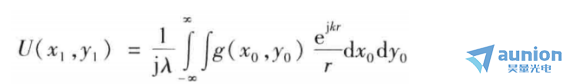
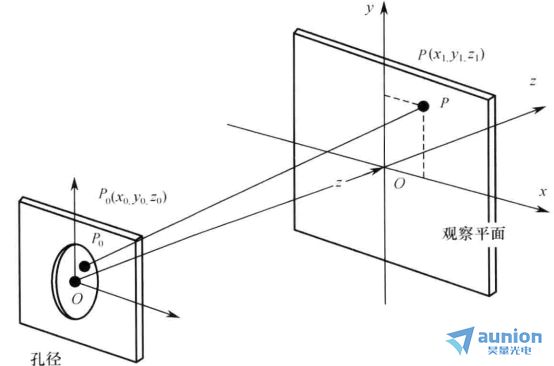
图2 孔径的衍射
当观察屏远离衍射孔径并且衍射孔径本身的尺度不是非常大时,r近似为:

如果上式中的前三项(在距离孔径比较远的位置观察衍射花样),称之为夫琅禾费衍射区域;如果式中的前四项(在距离孔径比较近的位置观察衍射花样),我们称之为菲涅耳衍射区域。
在实际计量应用中,更多地采用夫琅禾费衍射近似,即
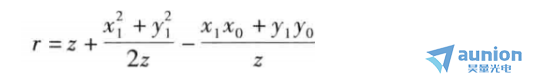
图3是衍射在计量中的一个应用例子,图中给出了单缝所产生的衍射图样。图中缝宽为a,在距离该孔径D(=z,且足够远)处的屏上,便可观察到其夫琅禾费衍射图样。此时U(x1,y1)为:
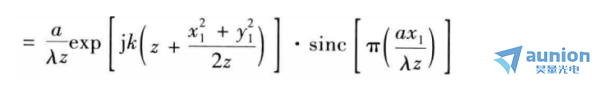
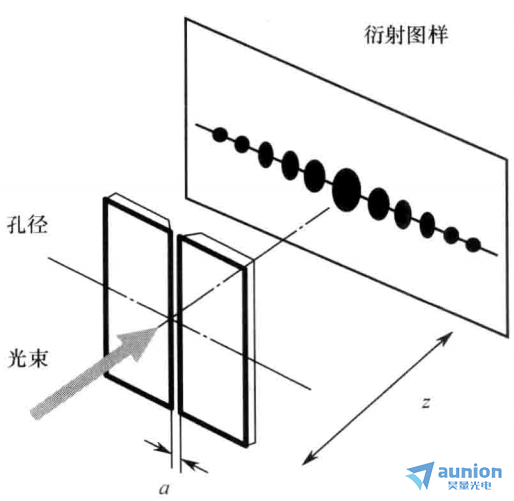
图3 单缝衍射
同上,大小为a×b的矩形孔衍射可表述为:
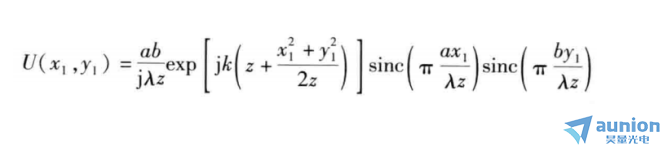
上式表明,衍射强度I(x)受到sinc函数的调制,其强度分布曲线如图4所示。
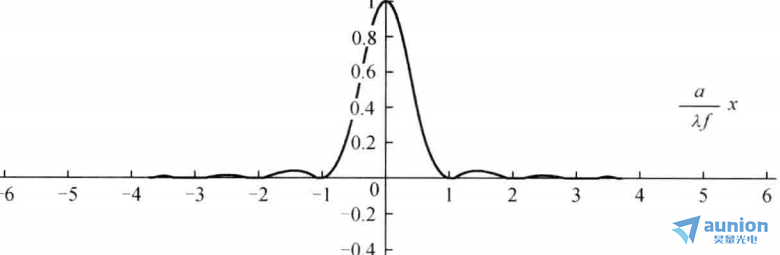
图4 衍射强度分布
从图中不难看出虽然衍射ji小间具有相同的间隔,但相邻的两个亮点之间的间隔并非严格相等。
了解更多详情,请访问上海昊量光电的官方网页:
https://www.auniontech.com/details-608.html
更多详情请联系昊量光电/欢迎直接联系昊量光电
关于昊量光电:
上海昊量光电设备有限公司是光电产品专业代理商,产品包括各类激光器、光电调制器、光学测量设备、光学元件等,涉及应用涵盖了材料加工、光通讯、生物医疗、科学研究、国防、量子光学、生物显微、物联传感、激光制造等;可为客户提供完整的设备安装,培训,硬件开发,软件开发,系统集成等服务。
您可以通过我们昊量光电的官方网站www.auniontech.com了解更多的产品信息,或直接来电咨询4006-888-532。
展示全部 
