Talbot效应
Talbot效应
1836年，Henry Fox Talbot发现，当平行光照射一个周期性的结构，传播一段距离后，仍旧能够恢复原来光强的形状，这段距离成为Tablot长度。
因为光束是一个周期性的结构，假设周期为L，那么可以将光束表述为
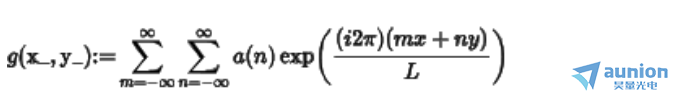
根据菲涅尔传播的公式，如果要计算光束的传播，需要分别对上述公式和表达式
求傅里叶变换，然后求卷积
对上述表达式求傅里傅里叶变换得到
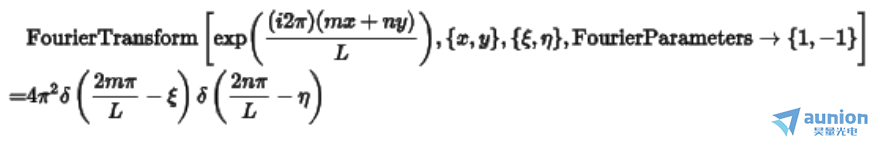
另一项傅里叶变换结果为
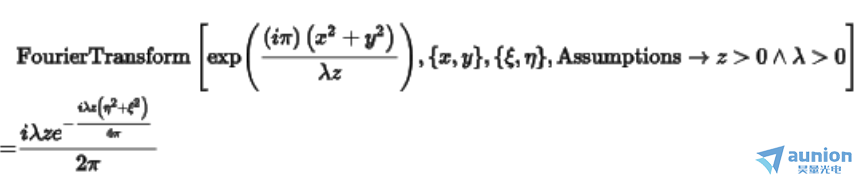
两项卷积后得到
因为公式中的u和v有各自的含义，分别带入后得到
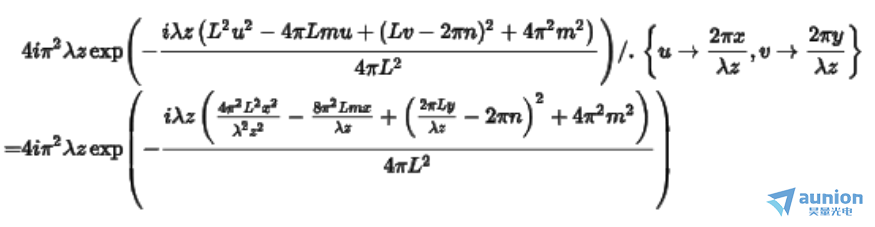
除了上述卷积表达式，还有其其他两项表达式，分别乘上去后简化得到
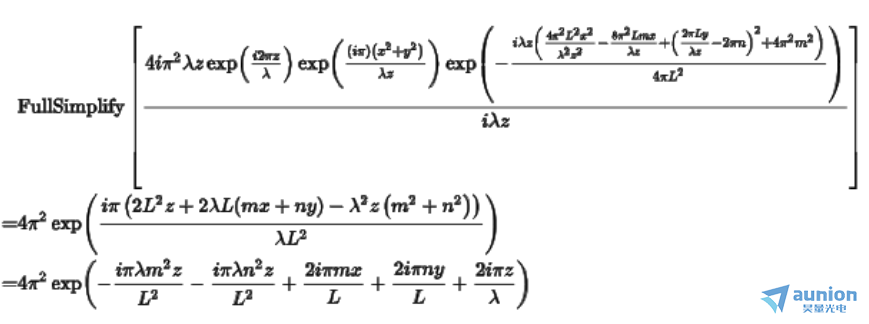
对比原先的表达式
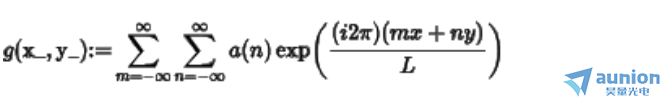
表达式中
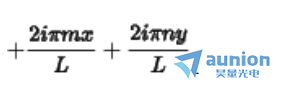这两项与原本公式相同
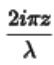:认为是一个常数项目
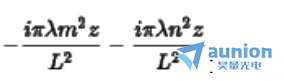当这一项的E指数变成为1时，那么就能够保持与输入光的相位相同，所以只有当
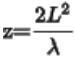的时候，可以保持输入光场和输出光场相同，所以在这个位置光强可以恢复原来分布。
举例
假设一个入射光分布为正弦分布，函数的周期为
，所以光强周期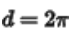
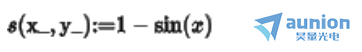
经过计算后，光强分布为
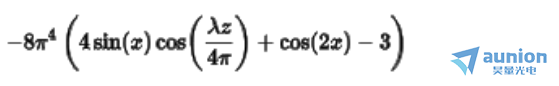
假设波长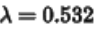
,所以Talbot长度为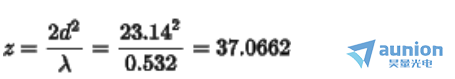
以x为纵轴，坐标范围为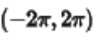
,z为横轴，坐标范围为
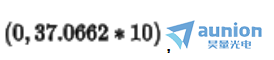那么整个光强分布为
了解更多详情，请访问上海昊量光电的官方网页：
https://www.auniontech.com/three-level-46.html
更多详情请联系昊量光电/欢迎直接联系昊量光电
关于昊量光电：
上海昊量光电设备有限公司是光电产品专业代理商，产品包括各类激光器、光电调制器、光学测量设备、光学元件等，涉及应用涵盖了材料加工、光通讯、生物医疗、科学研究、国防、量子光学、生物显微、物联传感、激光制造等；可为客户提供完整的设备安装，培训，硬件开发，软件开发，系统集成等服务。
您可以通过我们昊量光电的官方网站www.auniontech.com了解更多的产品信息，或直接来电咨询4006-888-532。
展示全部 
