

通过在相位型SLM上加载菲涅尔透镜,可以实现任意焦距。
透镜的相位变换作用
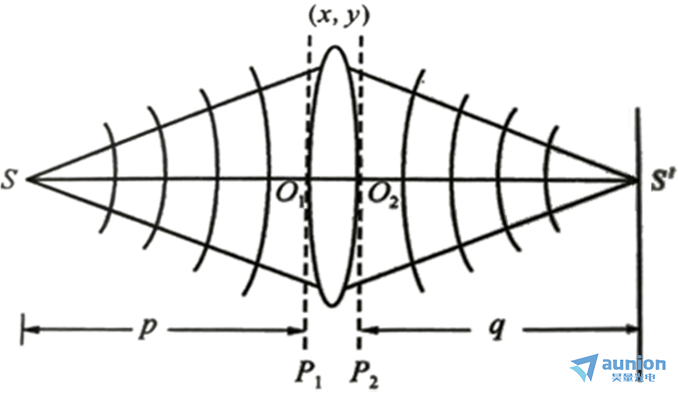
傍轴近似下,入射的单色点光源发出的球面波在薄透镜前表面上的复振幅分布为:
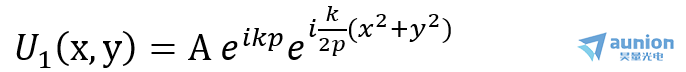
其中,A为振幅,k为波数,p为点光源到透镜的距离,x、y为当前面的横纵坐标轴上的位置。
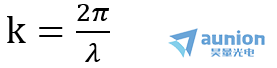
在透镜后表面上的复振幅分布为:
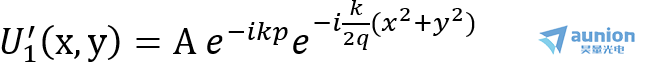
q 为像点到透镜的距离。
因此,透镜对前后表面的变换关系为:

由高斯成像公式:
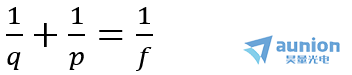
f 为透镜的像方焦距,由此,透镜的复振幅透过率变换因子t(x,y)可以表示为:
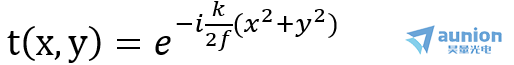
从透镜的透过率函数到SLM的相位图
在透镜的透过率函数中,e的复指数虚部实际为对相位的变换作用,因此,可以用相位型空间光调制器来实现透镜的功能,实际调制的相位φ为:
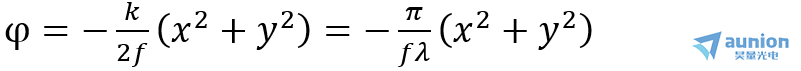
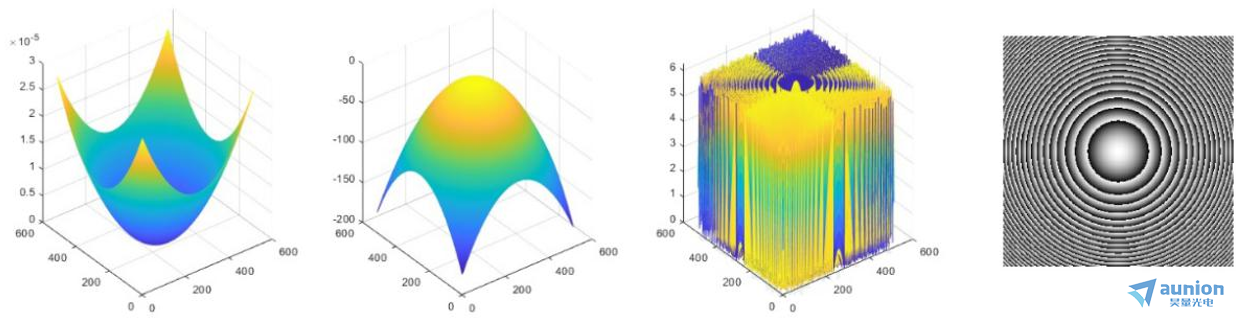
通过相位函数作相位图的过程为:
1.做出一副以中心为零点,图上每一点的值为到中心的横纵坐标x和y平方的和。
2.用上述相位函数做出图上每一点的相位调制量的相位图。
3.相位图上的调制量可能会大于 2π ,这时需要用菲涅尔透镜的原理将大于2π的值压缩到2π周期内。
4.将0—2π的相位转化为SLM对应的调制强度值(0—255)
透镜一般呈轴对称,(x^2+y^2 )等效为离轴距离r^2,上述函数可表示为
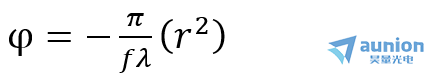
此外,调制相位量随r的变化还可以表示为其它更高级次的非球面或其它面型的透镜的函数。
您可以通过我们的官方网站了解更多的产品信息,或直接来电咨询4006-888-532。
展示全部 
展示全部 
