采用冯-诺依曼架构的现代电子产品的计算能力在本质上受到处理和存储单元之间数据传输速率的限制。如神经形态方法这样的新兴计算架构，通过将逻辑与内存交织在一起，是更有效的计算策略。近年来，光学手段再次被看作为完全或部分取代基于电子的计算机器的有希望的选择。其中，光计算尤其令人感兴趣，因为它每比特所需的能量以及延时都更少。2017 年，麻省理工学院的一组研究人员通过级联多个Mach-Zehnder干涉仪(MZI)在硅芯片上展示了一个突破性的、完全集成的光学神经网络(optical neural network,ONN)。通过计算每个MZI的相应相位，可以将任意矩阵有效地映射到该ONN硬件上。对于此类网络，所需的非线性可以通过利用强度调制器、相机的饱和效应、光电二极管的二次非线性、半导体放大器的饱和、可饱和吸收器等多种方法来实现。从那时起，人们提出了许多方案来进一步优化这些阵列的实现及其片上训练过程。
博览：2021 Optica 宇称时间对称光学神经网络
技术背景：
采用冯-诺依曼架构的现代电子产品的计算能力在本质上受到处理和存储单元之间数据传输速率的限制。如神经形态方法这样的新兴计算架构，通过将逻辑与内存交织在一起，是更有效的计算策略。近年来，光学手段再次被看作为完全或部分取代基于电子的计算机器的有希望的选择。其中，光计算尤其令人感兴趣，因为它每比特所需的能量以及延时都更少。2017 年，麻省理工学院的一组研究人员通过级联多个Mach-Zehnder干涉仪(MZI)在硅芯片上展示了一个突破性的、完全集成的光学神经网络(optical neural network,ONN)。通过计算每个MZI的相应相位，可以将任意矩阵有效地映射到该ONN硬件上。对于此类网络，所需的非线性可以通过利用强度调制器、相机的饱和效应、光电二极管的二次非线性、半导体放大器的饱和、可饱和吸收器等多种方法来实现。从那时起，人们提出了许多方案来进一步优化这些阵列的实现及其片上训练过程。
虽然 ONN 在学术和工业界中都受到了相当大的关注，但现在研究人员越来越意识到，改变芯片上的相位是不可取的，而且会显著掩盖光子加速器的潜在优势。在这些结构中，相位变化通常由热光移相器(thermo-optical phase shifter)实现(利用热光效应，通过施加偏置电流以改变光波导的折射率)。然而，由于大多数光电材料的热光系数相对较小，产生相位变化通常需要数十至数百微米数量级的路径长度。处理
位的数据，需要
个移相器，随着数据量的增加，这种方案可能会导致系统结构过大。此外，相位变化生效所需的时间相对较长，大约为数十微秒，这会限制片上(on chip)训练过程的速度(因为需要频繁地改变相位来计算梯度)。最近的一些工作旨在利用光学快速傅立叶变换 (OFFT)、环形谐振器、声光调制器和3D打印的替代架构来解决这些问题。其它基于相变材料、电吸收和电光效应的方法也可以解决其中的一些问题，但这些技术仍未成熟。
原理解析：
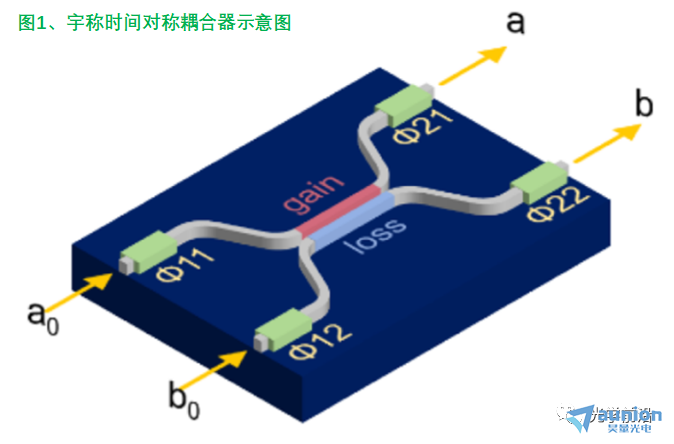
其输入与输出的关系为：
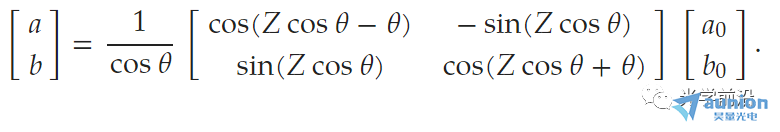
Z为常数，θ为与增益和损耗相关的需要训练得到的参数。这可以通过泵浦/载流子注入在标准III-V半导体系统中轻松实现。由于在空间、功耗和速度方面，改变增益-损耗系数比改变相位更有效，因此PT-ONN架构可潜在地需要更小的占用空间并以更低的功率加速片上训练。
(2)两层宇称时间对称ONN。如图2所示，在第一层，激光编码N1个像素，光信号首先被发送到由(N1(N1-1)/2)个宇称时间对称耦合器组成的三角形阵列。然后，光经过N2个放大器/衰减器，随后为由(N2(N2-1)/2)个宇称时间对称耦合器组成的第二个三角形阵列，然后是N2个非线性元件。第二层用星号表示，包含了相似的元件，但是有N2和N3值。该层终止于N3个光电探测器。值N1、N2、N3分别表示输入层、隐藏层和输出层的维度。光电探测器的输出发送到电子电路以计算PT耦合器增益损失参数，以在训练周期中实施梯度下降算法。
附录：
(1) Parity-Time对称理论(张亦弛 2019)
Parity-Time对称，简称PT对称，是源于量子力学中的概念，指的是系统的时间变换和宇称变换时对称的。在量子力学中，力学量通常用算符表示，而哈密顿算符(Hamiltonian)表示一个系统中的总能量。一般认为，一个可以观测到的物理量的算符必须满足厄密(Hermitian)对称条件，即某物理量矩阵满足共轭对称是保证其具有实数的特征值的充要条件。直到上世纪90年代末，C.M.Bender等人指出厄密对称只是物理量矩阵具有实数本征值的充分条件，并给出了一组新的对称条件。满足这组新的对称条件，单不满足厄密对称的哈密顿算符也可以具有实数本征值，这组新的对称条件即PT对称条件。
具体而言，当某个系统的哈密顿算符满足式(1.1)所示的条件时，就可以认为该系统满足PT对称条件。
的表达式通常含有空间变量和动量变量。
表示宇称变换，效果是将空间变量
和动量变量
同时反转，即
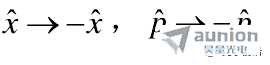
而
表示时间变换，它同时反转动量和虚数单位，即
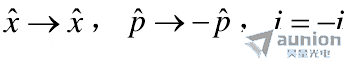
某个
是否满足PT对称条件，很大程度上由这个系统的势函数分布所决定。举个例子，设
为一非厄密对称的哈密顿算符，其中
为空间坐标，势函数
为复函数。根据上述对
和
的定义，很容易得到
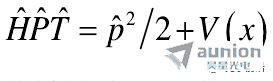
和
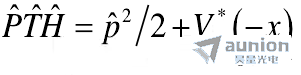
结合式(1.1)就可以将哈密顿算符的PT对称条件转换为势函数的对称条件
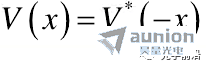
即系统的势函数在空间分布上必须是共轭复对称的。
参考文献：Haoqin Deng and Mercedeh Khajavikhan, "Parity–time symmetric optical neural networks," Optica 8, 1328-1333 (2021)
DOI：https://doi.org/10.1364/OPTICA.435525
关于昊量光电：
上海昊量光电设备有限公司是国内知名光电产品专业代理商，代理品牌均处于相关领域的发展前沿；产品包括各类激光器、光电调制器、光学测量设备、精密光学元件等，涉及应用领域涵盖了材料加工、光通讯、生物医疗、科学研究、国防及更细分的前沿市场如量子光学、生物显微、物联传感、精密加工、先进激光制造等；可为客户提供完整的设备安装，培训，硬件开发，软件开发，系统集成等优质服务。
您可以通过昊量光电的官方网站www.auniontech.com了解更多的产品信息，或直接来电咨询4006-888-532。
本文章经光学前沿授权转载,商业转载请联系获得授权。
展示全部 
