

摘要
具有低相位噪声的光学频率梳(OFC)可以在经典和量子系统中实现更严格的计量。为了消除相位噪声,必须扩展载波包络相位的反馈带宽和重复频率。在这里,我们提出了一种构建超低噪声OFC的方法。通过利用不同的电光调制器作为快速执行器,这种方法可以扩展反馈带宽超过150 kHz重复率的相位锁定和载波包络的抵消相位锁定,我们分别得到残余相位噪声21.8 mrad(18.1 as)和86.1mrad(71.3 as)的稳定光的击打信号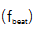 和载波包络的抵消频率
和载波包络的抵消频率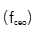 。我们通过测量两个梳齿之间的相对线宽来验证这个架构,它揭示了在1秒平均时间内,环内跳动的分数不稳定性小于
。我们通过测量两个梳齿之间的相对线宽来验证这个架构,它揭示了在1秒平均时间内,环内跳动的分数不稳定性小于 环外跳动的分数不稳定性小于
环外跳动的分数不稳定性小于 环外拍相位噪声为145 mrad (120 as)。这些结果表明,铒光纤激光技术与高带宽有效反馈相结合,可以保证在超低噪声条件下对光学基准进行相干跟踪。超低噪声OFC为高精度的、高分辨率的光谱学提供了一个通用的工具。
环外拍相位噪声为145 mrad (120 as)。这些结果表明,铒光纤激光技术与高带宽有效反馈相结合,可以保证在超低噪声条件下对光学基准进行相干跟踪。超低噪声OFC为高精度的、高分辨率的光谱学提供了一个通用的工具。
超快光源,可以发射一系列均匀间隔的飞秒脉冲,可以作为光学频率梳,提供微波和光域之间的相位相干链接[1,2]。任意纵向模式的频率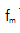 可以定义为
可以定义为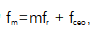 ,其中m为梳状线数(整数),
,其中m为梳状线数(整数), 为激光重复频率,
为激光重复频率, 为载波包络偏移(CEO)频率。这种技术的出现将光载波的相位控制技术扩展到光谱领域[3,4]。例如,精准的光学相位控制是光学原子钟铷钟[5 10]和物质量子态表征的关键元素[11 13]。虽然控制性能随着时间的推移有所改善,但仍需要本质低相位噪声锁模激光器,来满足高端基本时间常数变化应用研究的需求[14 16]。近期,长期相位稳定性和较佳噪声性能都在微波和光学频率之间的高精度合成中找到了新的应用,例如,在产生高纯微波的本振中,在同步激光微波网络中,以及在雷达系统中,[19]。对相位噪声性能的Z终限制的关键,是通过对两个自由度fr和fceo的波动来控制设定的。考虑
为载波包络偏移(CEO)频率。这种技术的出现将光载波的相位控制技术扩展到光谱领域[3,4]。例如,精准的光学相位控制是光学原子钟铷钟[5 10]和物质量子态表征的关键元素[11 13]。虽然控制性能随着时间的推移有所改善,但仍需要本质低相位噪声锁模激光器,来满足高端基本时间常数变化应用研究的需求[14 16]。近期,长期相位稳定性和较佳噪声性能都在微波和光学频率之间的高精度合成中找到了新的应用,例如,在产生高纯微波的本振中,在同步激光微波网络中,以及在雷达系统中,[19]。对相位噪声性能的Z终限制的关键,是通过对两个自由度fr和fceo的波动来控制设定的。考虑 和
和 基波波动对梳状线的贡献,各模态n的相位噪声功率谱密度(PSD)
基波波动对梳状线的贡献,各模态n的相位噪声功率谱密度(PSD)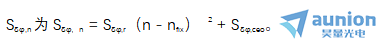 该表达式表明,单个梳模的相位波动是由这两个自由度的波动推导出来的。相位波动的影响对于扩大精密计量的范围至关重要。
该表达式表明,单个梳模的相位波动是由这两个自由度的波动推导出来的。相位波动的影响对于扩大精密计量的范围至关重要。
为了减少相位波动的影响,需要宽的动态范围和高调制带宽。通过使用快、慢压电传感器(PZTs)或电光调制器(EOMss),用于 控制的光学参考锁相(
控制的光学参考锁相(  稳定性)方案显然已经成熟[20-24],因此可以在超过10 kHz的频率范围内抑制相位噪声。该方案可以支持一个sub-MHz的响应带宽[23]。传统的稳定其他自由度
稳定性)方案显然已经成熟[20-24],因此可以在超过10 kHz的频率范围内抑制相位噪声。该方案可以支持一个sub-MHz的响应带宽[23]。传统的稳定其他自由度 的方法是通过泵浦电流调制[24-27]或腔外声光调制器[20,28,29]反馈误差信号来调节泵浦功率。可实现的带宽已扩展到100 kHz以上。受激寿命的长短主要取决于激光腔的增益和腔体的设计。然而,在许多应用中,降低
的方法是通过泵浦电流调制[24-27]或腔外声光调制器[20,28,29]反馈误差信号来调节泵浦功率。可实现的带宽已扩展到100 kHz以上。受激寿命的长短主要取决于激光腔的增益和腔体的设计。然而,在许多应用中,降低 在高频区域的快速相位波动是必要的,如标准传输[30,31]和高谐波产生[32,33]。
在高频区域的快速相位波动是必要的,如标准传输[30,31]和高谐波产生[32,33]。
为了抑制 的快速相位波动,人们已经研究了将锁相反馈带宽扩展到超出增益寿命限制的方法。采用更快的腔内损耗调制的调制器,如字素[34,35]和光学调制器[36],已被用于更快的控制。电光晶体可以为快速的相位波动提供亚兆赫的锁定带宽。然而,在光梳(OFC)中,使用不同腔内的EOMs抑制快速的相位波动的困难在于,当两个EOMs用于锁相时,不同腔内的EOMs制快速的相位波动的困难在于,当两个EOMs用于锁相时,不同腔内的EOMs会产生不必要的串扰。然而,通过将一个电光晶体与多个光学器件相结合,将相位调制转换为损耗调制,以减少亚兆赫兹反馈带宽下的这些不良影响。Menlo Systems在2015年展示了一种带有两个快速电光致动器的腔体,尽管他们没有给出腔体的细节[37,38]。
的快速相位波动,人们已经研究了将锁相反馈带宽扩展到超出增益寿命限制的方法。采用更快的腔内损耗调制的调制器,如字素[34,35]和光学调制器[36],已被用于更快的控制。电光晶体可以为快速的相位波动提供亚兆赫的锁定带宽。然而,在光梳(OFC)中,使用不同腔内的EOMs抑制快速的相位波动的困难在于,当两个EOMs用于锁相时,不同腔内的EOMs制快速的相位波动的困难在于,当两个EOMs用于锁相时,不同腔内的EOMs会产生不必要的串扰。然而,通过将一个电光晶体与多个光学器件相结合,将相位调制转换为损耗调制,以减少亚兆赫兹反馈带宽下的这些不良影响。Menlo Systems在2015年展示了一种带有两个快速电光致动器的腔体,尽管他们没有给出腔体的细节[37,38]。
本文提出了一种在掺铒光纤OFC系统中抑制相位噪声的方案。采用两个EOMs作为快速执行器,扩展了锁相反馈带宽,克服了腔动力学的限制。在谐振腔设计中,两种电磁谐振器使用不同的调制模式来降低串扰,达到了优化的目的。实现了在CEO频率和重复频率下都具有长期稳定和超低相位噪声性能的OFC。稳定的环内 显示在1 s平均时间下的分数不稳定性为
显示在1 s平均时间下的分数不稳定性为 积分剩余相位噪声为86.1 mrad (1Hz-1.5 MHz)。在1 s平均时间内,环内
积分剩余相位噪声为86.1 mrad (1Hz-1.5 MHz)。在1 s平均时间内,环内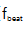 的分数不稳定性为
的分数不稳定性为 积分剩余相位噪声提高到21.8 mrad (1Hz-1.5 MHz)。利用两个OFC的相对线宽测量出环外外差拍频[25]。在1 s的平均时间内,出环
积分剩余相位噪声提高到21.8 mrad (1Hz-1.5 MHz)。利用两个OFC的相对线宽测量出环外外差拍频[25]。在1 s的平均时间内,出环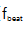 的分数不稳定性为
的分数不稳定性为 积分剩余相位噪声为145 mrad (1 Hz-1.5 MHz)。这些优异的性能表明反馈控制具有较高的精度;因此,我们的OFC是一个具有超低噪声应用和超精密测量的理想的振荡器。
积分剩余相位噪声为145 mrad (1 Hz-1.5 MHz)。这些优异的性能表明反馈控制具有较高的精度;因此,我们的OFC是一个具有超低噪声应用和超精密测量的理想的振荡器。
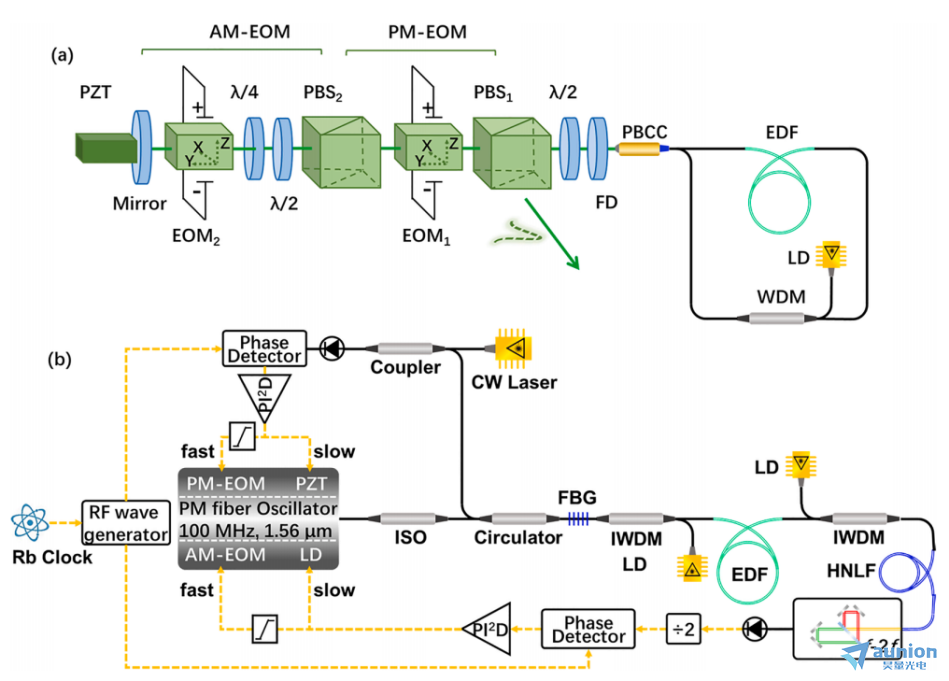
图1所示。(a)双EOMs锁模光纤激光器结构。FD,法拉第旋转器;PBCC,带偏振分束器的准直器;PBS,偏振分束器。(b)自参考稳定光纤频率梳实验装置总体方案。黑色线和黄色虚线分别表示光纤和电气连接。PM-EOMs,调相电光调制器;AM-EOMs,调幅电光调制器;ISO,隔离器;FBG、光纤布拉格光栅;IWDM,带隔离器的980/1550 nm波分复用器;LD, 976 nm激光二极管;法国电力公司(EDF), Er-doped纤维;高非线性光纤;连续波激光器,1560 nm的窄线宽连续波激光器。
图1(a)显示了两个EOMs的锁模光纤激光器结构,该结构采用非线性放大环镜(NALM)机制锁模。采用由偏振分束器(PBS)和准直器组成的集成器件来减小腔长。输出光束通过法拉第旋转器和半波片,在相位调制(PM)EOM中传输时,激光被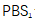 偏振。然后激光束在
偏振。然后激光束在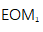 的X轴上保持偏振状态,通过改变相位调制电压来调制(PM)EOM的折射率。调幅(AM)EOM由PBS、半波片、四分之一波片、电光晶体和反射镜组成。反射镜安装在压电陶瓷上,以补偿腔长的长期变化。当X轴偏振光束发射到AM-EOM时,半波片将光束旋转45°,以获得Z轴和X轴上相等的分量。由于双折射效应,光束沿椭圆偏振,在四分之一波片和
的X轴上保持偏振状态,通过改变相位调制电压来调制(PM)EOM的折射率。调幅(AM)EOM由PBS、半波片、四分之一波片、电光晶体和反射镜组成。反射镜安装在压电陶瓷上,以补偿腔长的长期变化。当X轴偏振光束发射到AM-EOM时,半波片将光束旋转45°,以获得Z轴和X轴上相等的分量。由于双折射效应,光束沿椭圆偏振,在四分之一波片和 中旋转传播。仔细调整波片后,当反射光束到达
中旋转传播。仔细调整波片后,当反射光束到达 时,大部分激光功率仍停留在X轴上。PBS1作为一个分析仪,在Z轴向外反射激光功率。当调制电压加载在
时,大部分激光功率仍停留在X轴上。PBS1作为一个分析仪,在Z轴向外反射激光功率。当调制电压加载在 上时,Z轴和X轴之间的激光功率比发生变化,导致损耗调制。这种腔体设计保证了两个EOM在不同的工作模式下工作。一个EOM作为损耗相关的驱动器,另一个EOM作为相位相关的驱动器,以减少不良影响,实现完全稳定。超低噪声频率梳的布局如图1(b)所示。为尽量减少环境噪音,我们将OFC安装在铝盒内。光纤振荡器是一种环境稳定的掺铒光纤激光器,由保偏光纤(PMF)组成。
上时,Z轴和X轴之间的激光功率比发生变化,导致损耗调制。这种腔体设计保证了两个EOM在不同的工作模式下工作。一个EOM作为损耗相关的驱动器,另一个EOM作为相位相关的驱动器,以减少不良影响,实现完全稳定。超低噪声频率梳的布局如图1(b)所示。为尽量减少环境噪音,我们将OFC安装在铝盒内。光纤振荡器是一种环境稳定的掺铒光纤激光器,由保偏光纤(PMF)组成。
采用NALM锁模机制,获得了稳定的脉冲序列和自启动。利用一段正常色散的掺铒光纤平衡色散管理孤子产生的腔内色散。该振荡器在重复频率为100 MHz和泵浦功率为415 mW时,平均输出功率高达35 mW。图2(a)和(b)分别绘制了半峰全宽为21 nm、脉冲持续时间为2.3 ps的光谱和相应的强度自相关迹。带宽为0.2 nm的PMF Bragg光栅滤光梳齿约1560 nm。反射的梳齿被送入耦合器,用于光学外差拍信号 检测。发射的梳齿在单通掺铒光纤放大器的两端抽运,平均功率为1300mw。在平均功率为200 mW的情况下,采用优化的自相位调制将光谱拓宽至45.5 nm,通过一段反常色散的PMF产生一个自相关宽度为117 fs(高斯拟合为83 fs)的输出脉冲。图2(c)和(d)分别为压缩光脉冲的展宽谱和干扰自相关迹。
检测。发射的梳齿在单通掺铒光纤放大器的两端抽运,平均功率为1300mw。在平均功率为200 mW的情况下,采用优化的自相位调制将光谱拓宽至45.5 nm,通过一段反常色散的PMF产生一个自相关宽度为117 fs(高斯拟合为83 fs)的输出脉冲。图2(c)和(d)分别为压缩光脉冲的展宽谱和干扰自相关迹。
然后,放大的脉冲序列直接光纤耦合到一个1550px高度非线性锗硅酸盐光纤[41]。保持偏振的高度非线性光纤(HNLF)在放大波长上提供了反常色散,从而通过孤子裂变产生了一个倍频跨越的光谱。图2(e)显示了保持偏振的HNLF输出光谱,其范围为1000 ~ 2250 nm。由于保持偏振的HNLF相对较长,该结构具有一个倍频跨越谱。然而,我们仍然获得稳定的脉冲能量和光谱形状只使用PMF成分。倍频跨越频谱耦合到一个f-to-2f干涉仪,以稳定频率梳和特征的偏移频率梳子。当周期极化铌酸锂晶体长度为1 mm,极化周期为31.30 ~ 32.81μm时,输出光谱的红移边缘频率增加了一倍。这种可调设计使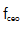 的信噪比(SNR)优化成为可能。在100 kHz的分辨率带宽下,检测到的
的信噪比(SNR)优化成为可能。在100 kHz的分辨率带宽下,检测到的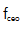 拍音信噪比为41dB,如图3(a)所示。然后,对来自10MHzRb原子钟的参考信号进行滤波、分割、放大和相位检测。使用数字-模拟混合Pi2D控制器将产生的误差信号转换为反馈信号。利用带宽为500 kHz的高压源放大的高频反馈信号驱动腔内AM-EOM进行快速调制。利用低频反馈信号作为驱动信号来控制泵电流。为了实现梳齿与基准激光器之间的锁相,我们将经过光纤布拉格光栅滤波的梳齿与单频激光器(OEwaves,线宽~ 10Hz)混合在PMF耦合器中。两束光聚焦在辫子状的光电二极管上后,得到的拍音信噪比为47 dB,分辨率带宽为100 kHz,如图3(b)所示。在
拍音信噪比为41dB,如图3(a)所示。然后,对来自10MHzRb原子钟的参考信号进行滤波、分割、放大和相位检测。使用数字-模拟混合Pi2D控制器将产生的误差信号转换为反馈信号。利用带宽为500 kHz的高压源放大的高频反馈信号驱动腔内AM-EOM进行快速调制。利用低频反馈信号作为驱动信号来控制泵电流。为了实现梳齿与基准激光器之间的锁相,我们将经过光纤布拉格光栅滤波的梳齿与单频激光器(OEwaves,线宽~ 10Hz)混合在PMF耦合器中。两束光聚焦在辫子状的光电二极管上后,得到的拍音信噪比为47 dB,分辨率带宽为100 kHz,如图3(b)所示。在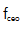 稳定中,
稳定中, 的转换误差信号被发送到PZT用于长腔漂移,并发送到腔内PM-EOM用于快速补偿振荡器长度。
的转换误差信号被发送到PZT用于长腔漂移,并发送到腔内PM-EOM用于快速补偿振荡器长度。
在OFC稳定之前,我们使用频率响应分析仪(Moku:Lab)测量了锁相环中执行器到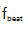 和
和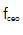 的传递函数。动态测量显示了
的传递函数。动态测量显示了 和
和 调制后的相关频率幅度和相位响应,如图4所示。PZT调制在7kHz时有一个3dB的角,而PM-EOM在156 kHz时有一个更高的角,如图4(a)所示。在
调制后的相关频率幅度和相位响应,如图4所示。PZT调制在7kHz时有一个3dB的角,而PM-EOM在156 kHz时有一个更高的角,如图4(a)所示。在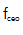 的频率响应轨迹中,泵浦电流调制在20 kHz时有一个3 dB的角,AM-EOM在161 kHz时有一个更高的角。值得注意的是,在泵电流作用下,AM-EOM具有不同的调制方式,其损耗调制特性与石墨烯调制相似[34]。
的频率响应轨迹中,泵浦电流调制在20 kHz时有一个3 dB的角,AM-EOM在161 kHz时有一个更高的角。值得注意的是,在泵电流作用下,AM-EOM具有不同的调制方式,其损耗调制特性与石墨烯调制相似[34]。
为了减少在完全稳定状态下四个执行器之间的不必要的串扰,我们优化了不同EOMs的腔体设计和调制模式。我们进行了时域分析,以揭示稳定的OFC的长期稳定性。使用Λ型频率计数器在门控时间为1秒的情况下计数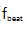 和
和 ,计数时间超过22小时。图5(A)显示了
,计数时间超过22小时。图5(A)显示了 的时间轨迹,其中分辨率受到频率计数器带宽的限制。
的时间轨迹,其中分辨率受到频率计数器带宽的限制。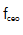 的偏移遵循2.1 ~ 2.1 mHz的正常跟踪,标准偏差265 μHz。图5(b)显示了测量到的
的偏移遵循2.1 ~ 2.1 mHz的正常跟踪,标准偏差265 μHz。图5(b)显示了测量到的 和参考时钟之间的频率差的直方图。数据分布呈高斯分布,宽度为524μHz。利用得到的
和参考时钟之间的频率差的直方图。数据分布呈高斯分布,宽度为524μHz。利用得到的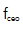 和
和 的数值(重叠的Allan偏差和修正的Allan偏差)来区分影响系统性能的噪声类型。如图5(c)所示,
的数值(重叠的Allan偏差和修正的Allan偏差)来区分影响系统性能的噪声类型。如图5(c)所示,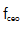 的重叠Allan偏差呈现出分数不稳定性,随着平均时间的增加,分数不稳定性从
的重叠Allan偏差呈现出分数不稳定性,随着平均时间的增加,分数不稳定性从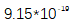 改善到
改善到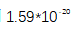 (误差条代表平均值的样本标准差)。随时间变化的斜率对光频率合成的波动非常敏感,表明
(误差条代表平均值的样本标准差)。随时间变化的斜率对光频率合成的波动非常敏感,表明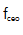 和Rb时钟之间存在紧密的锁相。在修正的Allan偏差分析中,计算的不稳定性分数在平均低于1000 s时也产生了
和Rb时钟之间存在紧密的锁相。在修正的Allan偏差分析中,计算的不稳定性分数在平均低于1000 s时也产生了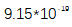 到
到 的斜率。对于较长的平均时间,不稳定性受到不必要的频闪噪声的限制。
的斜率。对于较长的平均时间,不稳定性受到不必要的频闪噪声的限制。
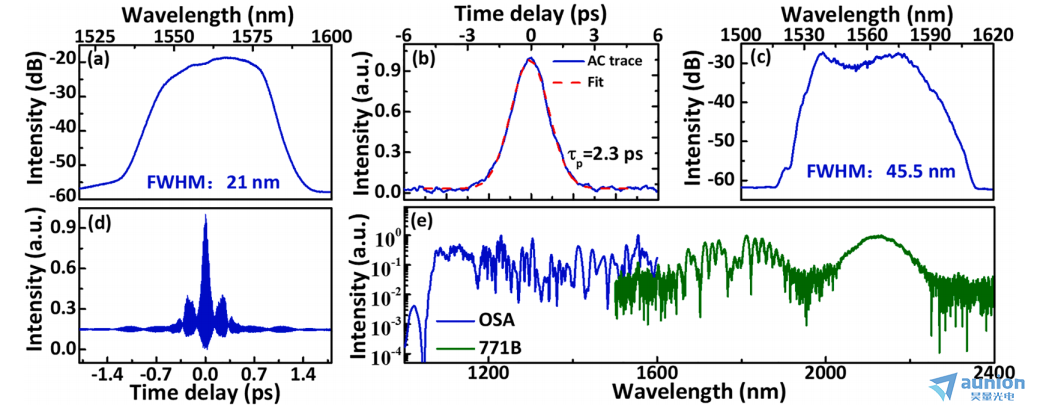
图2所示。(a)锁模铒光纤激光器的光谱范围为21 nm,中心为1560 nm。(b)强度自相关迹为2.3 ps脉冲。(c)放大后的光谱输出范围为45.5 nm。(d)压缩后83 fs脉冲的干扰自相关迹线。(e)两个光谱分析仪测量HNLF后的超连续统。

图3所示。(a)光电探测器检测到的fceo的射频频谱。(b)光电探测器检测到的光拍音符(fbeat)的RF频谱。
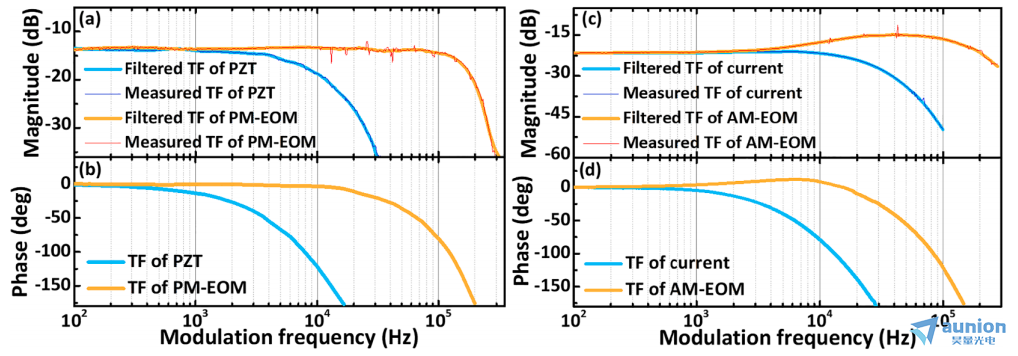
图4所示。从锁相环路中的PZT(蓝色)和PM-EOMs(橙色)到fbeat (a)幅值和(b)相位的传递函数。从锁相环中的泵电流(蓝色)和AM-EOMs(橙色)传递函数到(c)幅值和(d)相位的fceo。(细线为测量轨迹,粗线为拟合传递函数。)
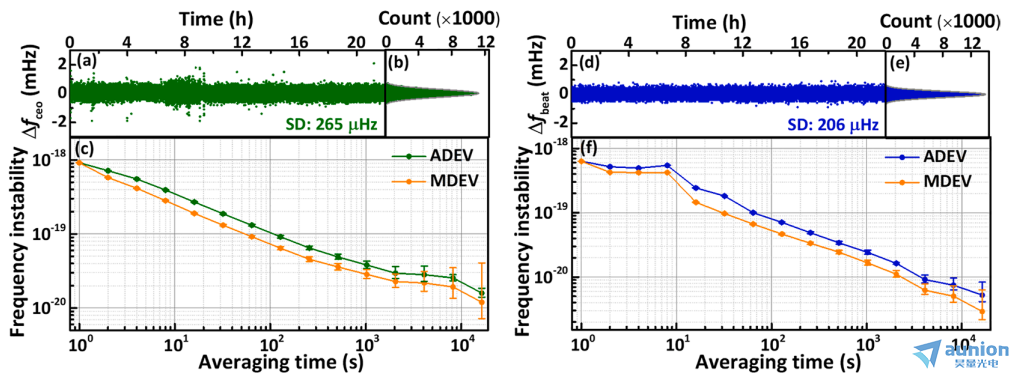
图5所示。(a)记录的时间序列和(b) fceo偏移量的计数。(c)将记录的fceo的Allan偏差重叠(绿色)和修正Allan偏差(橙色)。(d)记录的时间序列和(e) fbeat偏移量。(f)将记录的fbeat的Allan偏差(蓝色)和修正的Allan偏差(橙色)重叠。
计算得到的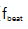 原始数据如图5(d)所示;在22h以上无相位滑移,标准偏差为206μHz。直方图分析表明,时间轨迹呈正态分布,高斯拟合结果为212μHz的宽度,如图5(e)所示。同样,
原始数据如图5(d)所示;在22h以上无相位滑移,标准偏差为206μHz。直方图分析表明,时间轨迹呈正态分布,高斯拟合结果为212μHz的宽度,如图5(e)所示。同样, 也是稳定的,如图5(f)所示。在短期平均时间,2 s<τ<10s时,重叠的Allan偏差和修正的Allan偏差均偏离期望斜率。自由运行的单频激光器是造成平均时间在2 ~ 10s之间呈平坦依赖性的主要原因。后来的闭环测量显示,通过将激光锁定在OFC上,消除了这种平坦性[图9(c)]。这表明差分噪声阻碍了相参平均,但它可以通过光程长度的抵消来降低。[43]得到了平均时间为1s时的分数不稳定性为
也是稳定的,如图5(f)所示。在短期平均时间,2 s<τ<10s时,重叠的Allan偏差和修正的Allan偏差均偏离期望斜率。自由运行的单频激光器是造成平均时间在2 ~ 10s之间呈平坦依赖性的主要原因。后来的闭环测量显示,通过将激光锁定在OFC上,消除了这种平坦性[图9(c)]。这表明差分噪声阻碍了相参平均,但它可以通过光程长度的抵消来降低。[43]得到了平均时间为1s时的分数不稳定性为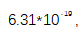 重叠的Allan偏差达到
重叠的Allan偏差达到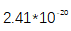 的不稳定性,在平均大于1000 s时没有明显的频偏。
的不稳定性,在平均大于1000 s时没有明显的频偏。
将锁模激光器的 和
和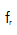 固定在一定的频率上,降低锁模激光器的相位噪声,是提高锁模激光器精密度的关键。为了改善系统的相位噪声性能,采用了大带宽驱动器与较佳净腔色散和泵浦电流相结合的方法。请注意,由射频参考信号直接稳定的OFC会随着光模式数量的增加而出现相位噪声退化,导致光线宽度变宽,也是高频抖动引起的。在我们的系统中,从梳状模与光学基准之间的拍频信号中提取出梳状模的相位波动。为了抑制快速的相位波动(>10kHz),同时获得长期稳定,通常都需要宽的动态范围和较高的调制带宽。为了通过光拍信号
固定在一定的频率上,降低锁模激光器的相位噪声,是提高锁模激光器精密度的关键。为了改善系统的相位噪声性能,采用了大带宽驱动器与较佳净腔色散和泵浦电流相结合的方法。请注意,由射频参考信号直接稳定的OFC会随着光模式数量的增加而出现相位噪声退化,导致光线宽度变宽,也是高频抖动引起的。在我们的系统中,从梳状模与光学基准之间的拍频信号中提取出梳状模的相位波动。为了抑制快速的相位波动(>10kHz),同时获得长期稳定,通常都需要宽的动态范围和较高的调制带宽。为了通过光拍信号 来控制重复频率
来控制重复频率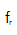 ,通过压电陶瓷来补偿由腔长变化引起的重复频率大而慢的偏移。利用PM-EOM实现了对相位噪声的快速抑制,提高了闭环增益和反馈带宽。
,通过压电陶瓷来补偿由腔长变化引起的重复频率大而慢的偏移。利用PM-EOM实现了对相位噪声的快速抑制,提高了闭环增益和反馈带宽。
图6(a)和(b)显示了重复频率稳定的过程,这是通过测量每个执行器打开时的20MHz节拍信号观察到的。完全稳定后在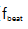 中观察到的强相干峰表明在光学参考线和梳状线之间获得了紧密的相位锁定。射频频谱和相位噪声中没有明显的伺服隆起。相位噪声的峰值出现在154kHz ~ 1.5MHz之间,是由EOM的机械共振引起的[21]。使用相位噪声分析仪(R&S FSWP8)分析了与锁定相关的相位噪声。
中观察到的强相干峰表明在光学参考线和梳状线之间获得了紧密的相位锁定。射频频谱和相位噪声中没有明显的伺服隆起。相位噪声的峰值出现在154kHz ~ 1.5MHz之间,是由EOM的机械共振引起的[21]。使用相位噪声分析仪(R&S FSWP8)分析了与锁定相关的相位噪声。
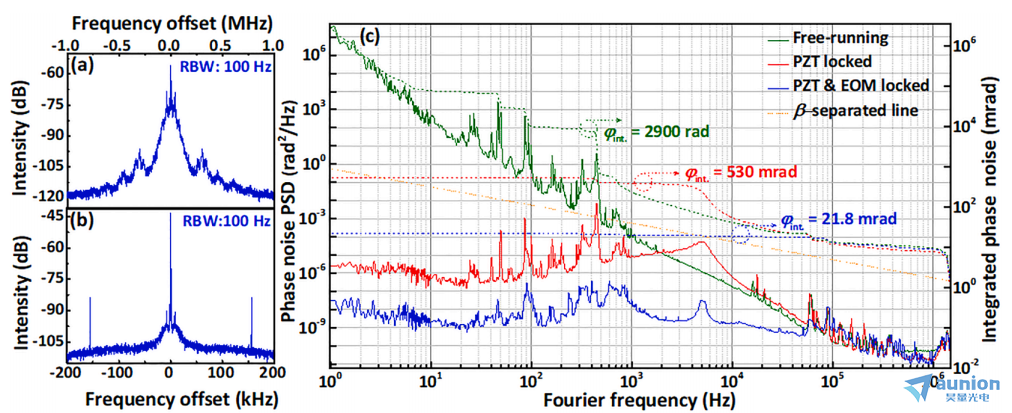
图6所示。(a)仅使用PZT稳定fbeat的环内射频频谱。(b)使用PZT和PM-EOM稳定fbeat的环内射频频谱。(c) fbeat的相位噪声特性:fbeat稳定使用PZT(红色实线),fbeat稳定使用PZT和PM-EOM(蓝色实线),积分的自由运行fbeat的相位噪声(绿色虚线),fbeat稳定使用PZT(蓝色虚线),使用PZT和PM-EOM(红色虚线)稳定fbeat。橙色虚线为引入β分离线。
图6(c)所示用实线表示自由运行、锁定和紧锁情况下的单边相位噪声PSD,用虚线表示相应的傅立叶频率降低的积分剩余相位噪声线。为了区分主线宽度对梳状线的贡献,我们在图6(c)中引入了β分离线(橙色虚线)。根据自由运行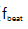 的相位噪声PSD与β分离线的交点,估计锁相所需的较小反馈带宽在500 Hz左右。在两种相位稳定的情况下,在自由运行拍信号的低频区,锁相环显著降低1/f频率噪声。在PZT锁定的情况下,只有一小部分相位噪声PSD在400 Hz左右高于β分离线,并贡献了梳状线宽。剩余环内积分相位噪声为530 mrad[图6(c)中的红虚线]。为了进一步扩大反馈带宽并实现更大的调制深度,只使用单个压电陶瓷的策略在实验上是具有挑战性的,其中在PZT支架上发生的共振是主要的限制因素。为了消除这种不良的共振,采用了具有更高反馈带宽的PM-EOM。在此条件下,利用这种高带宽EOM可以抑制由快速相位波动引起的7 kHz以上的相位噪声。此外,由于EOM可以抑制谐振,进一步提高了压电陶瓷的调制深度。当两种执行器串联调谐时,相位噪声PSD保持在β分离线以下。这种特性表明,剩余相位噪声不会对梳状线宽产生负面影响。得到积分剩余相位噪声21.8 mrad (1Hz-1.5MHz),脉冲对脉冲的时间抖动为18.1as。这一结果证明了梳状线能在超低噪声条件下相干跟踪光参考信号。
的相位噪声PSD与β分离线的交点,估计锁相所需的较小反馈带宽在500 Hz左右。在两种相位稳定的情况下,在自由运行拍信号的低频区,锁相环显著降低1/f频率噪声。在PZT锁定的情况下,只有一小部分相位噪声PSD在400 Hz左右高于β分离线,并贡献了梳状线宽。剩余环内积分相位噪声为530 mrad[图6(c)中的红虚线]。为了进一步扩大反馈带宽并实现更大的调制深度,只使用单个压电陶瓷的策略在实验上是具有挑战性的,其中在PZT支架上发生的共振是主要的限制因素。为了消除这种不良的共振,采用了具有更高反馈带宽的PM-EOM。在此条件下,利用这种高带宽EOM可以抑制由快速相位波动引起的7 kHz以上的相位噪声。此外,由于EOM可以抑制谐振,进一步提高了压电陶瓷的调制深度。当两种执行器串联调谐时,相位噪声PSD保持在β分离线以下。这种特性表明,剩余相位噪声不会对梳状线宽产生负面影响。得到积分剩余相位噪声21.8 mrad (1Hz-1.5MHz),脉冲对脉冲的时间抖动为18.1as。这一结果证明了梳状线能在超低噪声条件下相干跟踪光参考信号。
如图7(a)和(b)所示,在每个锁相情况下测量了稳定在20MHz的 信号。在两种锁定情况下,
信号。在两种锁定情况下, 的相干峰值在15 ~ 50 dB之间更强,表明AM-EOM的载波和包膜之间有紧密的相位锁定。当AM-EOM有助于锁定时,观察到20 kHz的伺服冲击,这与图4(c)中测量到的泵电流传递函数非常一致。在更高的频率范围内也没有伺服凸点,这类似于用损耗调制模式的石墨烯调制锁相用于
的相干峰值在15 ~ 50 dB之间更强,表明AM-EOM的载波和包膜之间有紧密的相位锁定。当AM-EOM有助于锁定时,观察到20 kHz的伺服冲击,这与图4(c)中测量到的泵电流传递函数非常一致。在更高的频率范围内也没有伺服凸点,这类似于用损耗调制模式的石墨烯调制锁相用于 稳定[33]。为了进一步展示AM-EOM在梳状偏移频率
稳定[33]。为了进一步展示AM-EOM在梳状偏移频率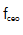 处作为快速执行器的性能,我们测量了相位噪声PSD来检测相位噪声抑制。在两种情况下
处作为快速执行器的性能,我们测量了相位噪声PSD来检测相位噪声抑制。在两种情况下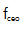 稳定,频率噪声在自由运行的fceo低频区被抑制。两相噪声PSD线在整个测量频率范围内都保持在β分离线以下,表明剩余相位噪声对
稳定,频率噪声在自由运行的fceo低频区被抑制。两相噪声PSD线在整个测量频率范围内都保持在β分离线以下,表明剩余相位噪声对 线宽的贡献很小;这一结果与图7(a) (b)中实测的
线宽的贡献很小;这一结果与图7(a) (b)中实测的 信号有很好的一致性。在只有泵电流的锁相情况下,计算出
信号有很好的一致性。在只有泵电流的锁相情况下,计算出 的剩余积分相位噪声为419.6 mrad[图7(c)中的红虚线]。泵浦电流调制所能达到的带宽受受激寿命的限制,是由增益介质和激光腔设计决定的。AM-EOM的使用是一种有效的
的剩余积分相位噪声为419.6 mrad[图7(c)中的红虚线]。泵浦电流调制所能达到的带宽受受激寿命的限制,是由增益介质和激光腔设计决定的。AM-EOM的使用是一种有效的 稳定方案,以克服限制和扩大反馈带宽。由于AM-EOM可以作为快速致动器,直接损耗调制可以实现脉冲能量的即时变化,并具有更高的响应带宽,这有可能超过受激寿命限制。对于泵电流和AM-EOM锁定,成功地降低了超过8kHz的快速相位波动。泵电流锁相曲线和电流锁相曲线与AM-EOM在20 kHz和200 kHz处相交,表示电流与AM-EOM存在竞争。
稳定方案,以克服限制和扩大反馈带宽。由于AM-EOM可以作为快速致动器,直接损耗调制可以实现脉冲能量的即时变化,并具有更高的响应带宽,这有可能超过受激寿命限制。对于泵电流和AM-EOM锁定,成功地降低了超过8kHz的快速相位波动。泵电流锁相曲线和电流锁相曲线与AM-EOM在20 kHz和200 kHz处相交,表示电流与AM-EOM存在竞争。 的积分剩余相位噪声降低到86.1 mrad [1hz-1.5 MHz,图7(c)中的蓝虚线],对应的定时抖动为71.3 as。由于AM-EOM设备在激光腔中进行损耗调制,因此我们也研究了
的积分剩余相位噪声降低到86.1 mrad [1hz-1.5 MHz,图7(c)中的蓝虚线],对应的定时抖动为71.3 as。由于AM-EOM设备在激光腔中进行损耗调制,因此我们也研究了 的振幅噪声,如图7(d)所示。AM-EOM抑制了1 ~ 80 kHz的振幅噪声,而80 ~ 300 kHz的噪声由于锁相带宽限制而增加。噪声性能证明了该方案在两个EOM中实现OFC锁相的潜力。
的振幅噪声,如图7(d)所示。AM-EOM抑制了1 ~ 80 kHz的振幅噪声,而80 ~ 300 kHz的噪声由于锁相带宽限制而增加。噪声性能证明了该方案在两个EOM中实现OFC锁相的潜力。
对这种锁相方法中的环外跳动进行了评估,表明该梳状滤波器适合于需要低噪声的应用[25,45-48]。图8为测量梳齿出环拍的实验装置。从梳由1560 nm的单频连续激光器组成的桥接锁相与主梳相连接。用另一个1545nm的单频连续激光器来表征相对光梳线噪声。主梳是一个稳定的OFC,指的是一个Rb时钟到锁相 和
和 。该方法比较了两个梳齿之间的相对线宽,消除了连续波激光器[25]的限制。由单频激光组成的桥接将从梳与主梳锁相。利用f-2f方法对从梳的f0值进行锁相。主梳和从梳的CEO都是锁相的,并结合泵电流和AM-EOM。从梳的残余CEO与主梳相似,如图7 (c)所示。
。该方法比较了两个梳齿之间的相对线宽,消除了连续波激光器[25]的限制。由单频激光组成的桥接将从梳与主梳锁相。利用f-2f方法对从梳的f0值进行锁相。主梳和从梳的CEO都是锁相的,并结合泵电流和AM-EOM。从梳的残余CEO与主梳相似,如图7 (c)所示。

图7所示。(a)仅使用泵电流稳定fceo的环内射频频谱。(b)使用泵电流和AM-EOM稳定fceo的环内射频频谱。(c) fceo的相位噪声特性:相位噪声的不同步的fceo(绿色实线),fceo稳定只使用泵电流(红色实线),并使用泵fceo稳定电流和AM-EOM(蓝色实线)和综合相位噪声的不同步的fceo(绿色虚线),fceo稳定只使用泵电流(蓝色虚线),fceo使用泵电流和AM-EOM(红色虚线)稳定下来。橙色虚线为β分离线。(d) fceo的噪声强度表征。
两个梳梳之间在1545nm的拍频信号由另一个单频激光(OEwaves, 1545nm)提取,这也用于表征环外性能。环外拍会受到我们选择测量的波长的影响。两个梳之间的相对线宽会随着测量波长远离锁定点而增加[49]。泵浦激光诱导的RIN主要影响梳齿线宽的增宽。量子极限、环境噪声和空腔损耗波动也会导致线宽的增加。噪声会随着梳齿远离锁相波长而增加。
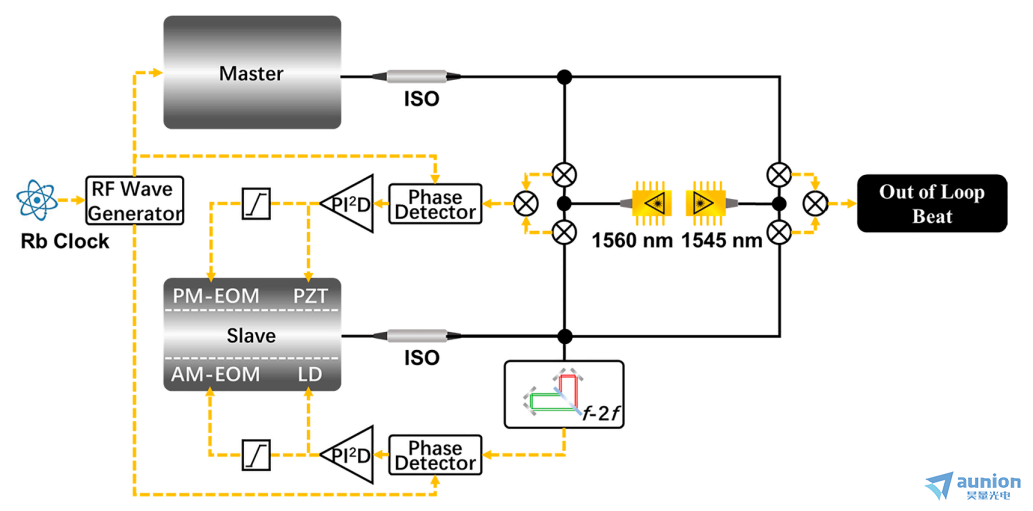
图8所示。实验设置测量OFC的环外跳动使用射频锁定OFC作为参考。主梳的载波包络偏移和重复频率被锁相到Rb时钟。从梳由1560 nm的单频激光组成的桥接锁相到主梳。利用1545 nm的单频激光器作为桥接测量环外拍,揭示了梳状结构中两个EOM的锁相能力。
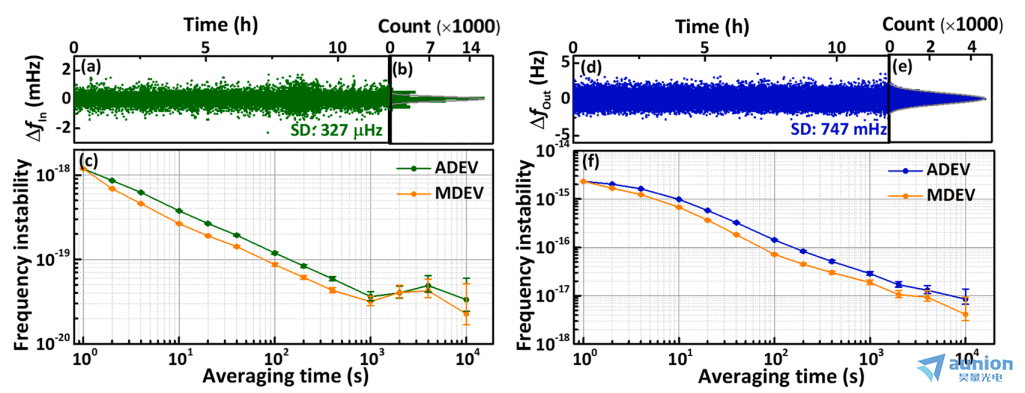
图9所示。(a)记录的时间序列和(b) f1560偏移的计数。(c)将记录的f1560的Allan偏差(绿色)与修正后的Allan偏差(橙色)重叠。(d)记录的时间序列和(e) f1545偏移量的计数。(f)记录的f1545重叠Allan偏差(蓝色)和修正Allan偏差(橙色)。
用于评估该梳状结构的环外性能的方法与文献[39]中的方法相似。原始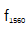 计数如图9(a)所示,在超过12小时内没有相位滑移。计算的标准偏差为327μHz。图9(b)和(c)为环路外差拍
计数如图9(a)所示,在超过12小时内没有相位滑移。计算的标准偏差为327μHz。图9(b)和(c)为环路外差拍 的直方图和重叠Allan偏差。环内不稳定性在平均1 s时为
的直方图和重叠Allan偏差。环内不稳定性在平均1 s时为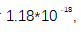 在平均1000s时为
在平均1000s时为 。平均时间较长时,出现频闪现象,与图5(c)相似。由于两个梳齿的噪声叠加,精度略有下降。当环内拍f1560紧锁相时,环外拍f1545同时被记录。图9(d)显示了外环外差拍
。平均时间较长时,出现频闪现象,与图5(c)相似。由于两个梳齿的噪声叠加,精度略有下降。当环内拍f1560紧锁相时,环外拍f1545同时被记录。图9(d)显示了外环外差拍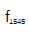 的实测频率偏移。一个12小时的记录显示标准偏差为747 mHz。图9(e)是环路外拍
的实测频率偏移。一个12小时的记录显示标准偏差为747 mHz。图9(e)是环路外拍 的直方图。所测
的直方图。所测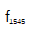 的重叠Allan偏差如图9(f)所示;在平均1 s的时间内,分数不稳定性为
的重叠Allan偏差如图9(f)所示;在平均1 s的时间内,分数不稳定性为 在10000 s平均时间内,分数不稳定性提高到
在10000 s平均时间内,分数不稳定性提高到 。噪音部分可归因于OFC的不完善。每个分支也会产生不同的噪声,如参考文献[39]所述。我们分析射频信号的频谱和相位噪声,以验证能力稳定梳使用我们的方法。图10 (a)和(b)分别显示了稳定后的
。噪音部分可归因于OFC的不完善。每个分支也会产生不同的噪声,如参考文献[39]所述。我们分析射频信号的频谱和相位噪声,以验证能力稳定梳使用我们的方法。图10 (a)和(b)分别显示了稳定后的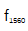 和
和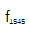 在100 Hz分辨率带宽下的射频频谱。在这种紧密锁相方法中,图10(a)和(b)得到了环内和环外拍的高相干峰值。图10(c)显示了环内和环外的相位噪声和剩余相位波动。相应的环内 f1560(蓝虚线)的积分相位噪声为25.9 mrad (21.4 as,从1hz积分到1.5 MHz)。此外,环外跳动
在100 Hz分辨率带宽下的射频频谱。在这种紧密锁相方法中,图10(a)和(b)得到了环内和环外拍的高相干峰值。图10(c)显示了环内和环外的相位噪声和剩余相位波动。相应的环内 f1560(蓝虚线)的积分相位噪声为25.9 mrad (21.4 as,从1hz积分到1.5 MHz)。此外,环外跳动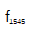 (红色虚线)相位噪声为145 mrad (120 as,集成从1 Hz到1.5 MHz)。离环拍的剩余相位噪声集中在低频波段,主要是由不同分支光纤[43]中的声噪声和温度噪声引起的。
(红色虚线)相位噪声为145 mrad (120 as,集成从1 Hz到1.5 MHz)。离环拍的剩余相位噪声集中在低频波段,主要是由不同分支光纤[43]中的声噪声和温度噪声引起的。
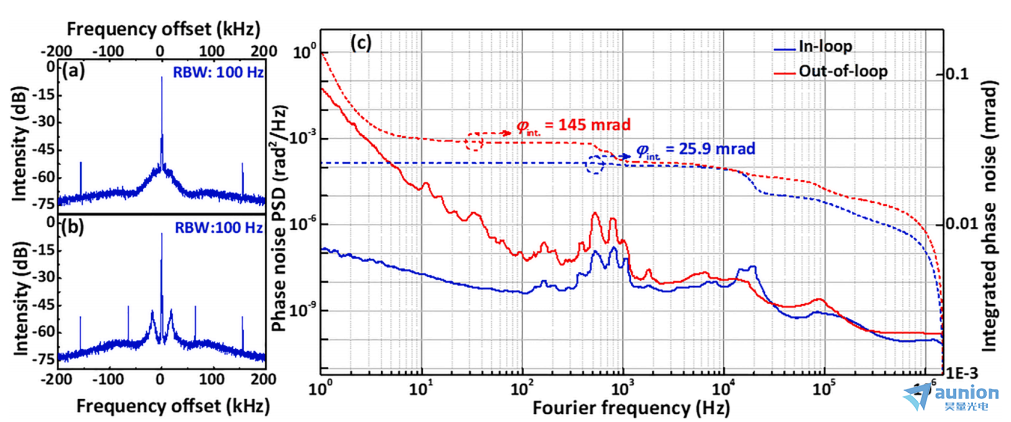
图10所示。(a)使用PZT和EOM稳定的在环拍Δf1560的射频频谱。(b)环外拍f1545的RF频谱。(c)环内f1560(蓝实线)和环外f1545(红实线)的相位噪声特性,环内拍(蓝虚线)和环外拍(红虚线)的积分相位噪声。
总之,我们开发、实现并描述了一种在自参考PM掺铒光纤OFC系统中抑制累积相位噪声的强大方法。实验中,我们使用了两个由EOM构造的快速驱动器,克服了腔动力学的限制,延长了锁相带宽。利用该方法实现了在载波包络相位偏移频率和重复频率下具有超低相位噪声的长期稳定OFC。我们使用环内测量来证明 和
和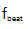 的不稳定性分数在1秒平均时间(Λ型计数器)分别为
的不稳定性分数在1秒平均时间(Λ型计数器)分别为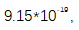 和
和 此外,通过测量两个梳齿的相对线宽,发现紧锁相后,在平均1 s的时间内,失环分数不稳定性为
此外,通过测量两个梳齿的相对线宽,发现紧锁相后,在平均1 s的时间内,失环分数不稳定性为 这些结果表明,参考梳子的稳定性是通过梳子线传递的。然后,这些测量结果表明,我们的超低相位噪声光纤OFC可以提供与基于Ti:蓝宝石激光器的OFC相媲美的性能。当我们的系统集成到OFC[50]中,我们的系统可以广泛应用于应用和基础物理,如宽带分子指纹光谱[51],基本量子动力学研究[52],超快纳米光子学[53]。
这些结果表明,参考梳子的稳定性是通过梳子线传递的。然后,这些测量结果表明,我们的超低相位噪声光纤OFC可以提供与基于Ti:蓝宝石激光器的OFC相媲美的性能。当我们的系统集成到OFC[50]中,我们的系统可以广泛应用于应用和基础物理,如宽带分子指纹光谱[51],基本量子动力学研究[52],超快纳米光子学[53]。
相关文献:
[1] S.T. Cundiff, J. Ye, J.L. Hall,rev. Sci. Instr. 72 (2001) 3749–3771.
[2]r.J. Jones, J.C. Diels, Phys.rev. Lett. 86 (2001) 3288–3291.
[3] D.J. Jones, S.A. Diddams, J.K.ranka, A. Stentz,r.S. Windeler, J.L. Hall, S. T. Cundiff, Science 288 (2000) 635–639.
[4]r. Holzwarth, T.h. Udem, T.W. H¨ansch, J.C. Knight, W.J. Wadsworth, P. St, J.russell, Phys.rev. Lett. 85 (2000) 2264–2267.
[5] A.D. Ludlow, M.M. Boyd, J. Ye, E. Peik, P.O. Schmidt,rev. Mod. Phys. 87 (2015) 637.
[6] M. Takamoto, F. Hong,r. Higashi, et al., An optical lattice clock, Nature 435 (2005) 321–324.
[7] N. Hinkley, J.A. Sherman, N.B. Phillips, M. Schioppo, N.D. Lemke, K. Beloy, M. Pizzocaro, C.W. Oates, A.D. Ludlow, Science 341 (2013) 1215–1218.
[8] B.J. Bloom, T.L. Nicholson, J.R. Williams, S.L. Campbell, M. Bishof, X. Zhang, W. Zhang, S.L. Bromley, J. Ye, Nature 506 (2014) 71–75.
[9] I. Ushijima, M. Takamoto, M. Das, T. Ohkubo, H. Katori, Nat. Photonics 9 (2015) 185–189.
[10] M. Schioppo,r.C. Brown, W.F. McGrew, N. Hinkley,r.J. Fasano, K. Beloy, T. H. Yoon, G. Milani, D. Nicolodi, J.A. Sherman, N.B. Phillips, C.W. Oates, A. D. Ludlow, Nat. Photonics 11 (2017) 48–52.
[11] A.S. Alnaser1, M. Kubel,r. Siemering, B. Bergues, Nora G. Kling, K. J. Betsch, Y. Deng, J. Schmidt, Z.A. Alahmed, A.M. Azzeer, J. Ullrich, I. Ben-Itzhak,r. Moshammer, U. Kleineberg, F. Krausz,r. de Vivie-Riedle, M.F. Kling, Nat. Commun. 5 (2014) 3800.
[12] M. Wollenhaupt, T. Baumert, Farad. Discuss. 153 (2011) 9–26.
[13] Deborah S. Jin, J. Ye, Chem.rev. 112 (2012) 4801–4802.
[14] A. Derevianko, M. Pospelov, Nat. Phys. 10 (2014) 933–936.
[15] S. Kolkowitz, I. Pikovski, N. Langellier, M.D. Lukin,r.L. Walsworth, J. Ye, Phys.rev. D 94 (2016) 124043.
[16] J. Grotti, S. Koller, S. Vogt, S. Hafner, U. Sterr, C. Lisdat, H. Denker, C. Voigt, L. Timmen, A.rolland, F. Baynes, H. Margolis, M. Zampaolo, P. Thoumany, M. Pizzocaro, B.rauf, F. Bregolin, A. Tampellini, P. Barbieri, M. Zucco, S. Costanzo, C. Clivati, F. Levi, D. Calenico, Nat. Phys. 14 (2018) 437–441.
[17] X. Xie,r. Bouchand, D. Nicolodi, M. Giunta, W. H¨ansel, M. Lezius, A. Joshi, S. Datta, C. Alexandre, M. Lours, P.-A. Tremblin, G. Santarelli,r. Holzwarth, Y. Le Coq, Nat. Photon. 11 (2017) 44–47.
[18] M. Xin, K. Safak, M.Y. Peng, A. Kalaydzhyan, W.-T. Wang, O.D. Mücke, F.X. K¨artner, Attosecond precision multi-kilometer laser-microwave network, Light Sci. Appl. 5 (2017) 16187.
[19] P. Ghelfi, F. Laghezza, F. Scotti, G. Serafino, A. Capria, S. Pinna, D. Onori, C. Porzi, M. Scaffardi, A. Malacarne, V. Vercesi, E. Lazzeri, F. Berizzi, A. Bogoni, Nature 507 (2014) 341–345.
[20] C. Benko, A.ruehl, M.J. Martin, K.S.E. Eikema, M.E. Fermann, I. Hartl, J. Ye, Opt. Lett. 37 (2012) 2196–2198.
[21] K. Iwakuni, H. Inaba, Y. Nakajima, T. Kobayashi, K. Hosaka, A. Onae, F.-L. Hong, Opt. Express 20 (2012) 13769–13776.
[22] L.C. Sinclair, J.D. Deschˆenes, L. Sonderhouse, W.C. Swann, I.H. Khader, E. Baumann, N.R. Newbury, I. Coddington,rev. Sci. Instrum. 86 (2015) 081301.
[23] Y. Ma, B. Xu, H. Ishii, F. Meng, Y. Nakajima, I. Matsushima, T.R. Schibli, Z. Zhang, K. Minoshima, Opt. Lett. 43 (2018) 4136–4139.
[24] J.J. McFerran, W.C. Swann, B.R. Washburn, N.R. Newbury, Opt. Lett. 31 (2006) 1997–1999.
[25] F. Adler, K. Moutzouris, A. Leitenstorfer, H. Schnatz, B. Lipphardt, G. Grosche, F. Tauser, Opt. Express 12 (2004) 5872–5880.
[26] S.A. Meyer, J.A. Squier, S.A. Diddams, Eur. Phys. J. D. 48 (2008) 19–26.
[27] M. Endo, T.D. Shoji, T.R. Schibli, IEEE JSTQE. 24 (2018) 1102413.
[28] T.M. Fortier, A. Bartels, S.A. Diddams, Opt. Lett. 31 (2006) 1011.
[29] K. Nakamura, S. Okubo, M. Schramm, K. Kashiwagi, H. Inaba, Appl. Phys. Express 10 (2017) 072501–072505.
[30] J. Ye, J.-L. Peng,r.J. Jones, K.W. Holman, J.L. Hall, D.J. Jones, S.A. Diddams, J. Kitching, S. Bize, J.C. Berquist, L.W. Hollberg, L.robertsson, L.-S. Ma, J. Opt. Soc. Am. B 20 (2003) 1459–1467.
[31] E. Chae, K. Nakashima, T. Ikeda, K. Sugiyama, K. Yoshioka, Opt. Express 27 (2019) 15649–15661.
[32]r. Kienberger, M. Hentschel, C. Spielmann, G.A.reider, N. Milosevic, U. Heinzmann, M. Drescher, F. Krausz, Appl. Phys B 74 (2002) S3–S9.
[33] N. Ishii, K. Kaneshima, K. Kitano, T. Kanai, S. Watanabe, J. Itatani, Nat Commun 5 (2014) 3331.
[34] C.-C. Lee, C. Mohr, J. Bethge, S. Suzuki, M.E. Fermann, I. Hartl, T.R. Schibli, Opt. Lett. 37 (2012) 3084–3086.
[35] N. Kuse, C.-C. Lee, J. Jiang, C. Mohr, T.R. Schibli, M.E. Fermann, Opt. Express 23 (2015) 24342–24350.
[36] M. Hoffmann, S. Schilt, T. Südmeyer, Opt. Express 21 (2013) 30054–30064.
[37] . H¨ansel, M. Giunta, K. Beha, M. Lezius, M. Fischer, andr. Holzwarth, Advanced solid state lasers Conference, paper ATh4A.2, 2015.
[38] M. Giunta, W. H¨ansel, K. Beha, M. Fischer, M. Lezius,r. Holzwarth, CLEO, paper STh4H.1, 2016.
[39] Y. Nakajima, H. Inaba, K. Hosaka, K. Minoshima, A. Onae, M. Yasuda, T. Kohno, S. Kawato, T. Kobayashi, T. Katsuyama, F. Hong, Opt. Express 18 (2010) 1667–1676.
[40] T. Yu, E.A. Golovchenko, A.N. Pilipetskii, C.R. Menyuk, Opt. Lett. 22 (1997) 793.
[41] M. Hirano, T. Nakanishi, T. Okuno, M. Onishi, IEEE J. Sel. Top. Quantum Electron. 15 (2009) 103–113.
[42] L. Yin, Q. Lin, G.P. Agrawal, Opt. Lett. 32 (2007) 391–393.
[43] D.R. Carlson, D.D. Hickstein, W. Zhang, A.J. Metcalf, F. Quinlan, S.A. Diddams, S. B. Papp, Science 361 (2018) 1358–1363.
[44] T.C. Briles, D.C. Yost, A. Cing¨oz, J. Ye, T.R. Schibli, Opt. Express 18 (2010) 9739.
[45] H. Leopardi, J. Davila-Rodriguez, F. Quinlan, J. Olson, J.A. Sherman, S. A. Diddams, T.M. Fortier, Optica 4 (2017) 879–885.
[46] M.J. Martin, S.M. Foreman, T.R. Schibli, Jun Ye, Opt. Express 17 (2009) 558–568.
[47] Gabriel Ycas, Steve Osterman, Scott A. Diddams, Opt. Lett. 37 (2012) 2199–2201.
[48] F. Adler, A. Sell, F. Sotier,r. Huber, A. Leitenstorfer, Opt. Lett. 32 (2007) 3504–3506.
[49] N.R. Newbury, W.C. Swann, J. Opt. Soc. Am. B 24 (2007) 1756–1770.
[50] S. Koke1, C. Grebing, H. frei, A. Anderson and A. Assion, Nat. Photonics 4 (2010) 462-465.
[51] H. Timmers, A. Kowligy, A. Lind, F.C. CRUZ, N. Nader and M. Silfies, Optica 5 (2018) 727-732.
[52] C.riek, P. Sulzer, M. Seeger, A.S. Moskalenko, G. Burkard, D.V. Seletskiy, A. Leitenstorfer, Nature 541 (2017) 376–385.
[53] L. Shi, B. Iwan,r. Nicolas, Q.ripault, J.R.C. Andrade, S. Han, H. Kim, W. Boutu, D. franz, T. Heidenblut, C.reinhardt, B. Bastiaens, T. Nagy, I. Babushkin, U. Morgner, S.W. Kim, G. Steinmeyer, H. Merdji, M. Kovacev, Optica 4 (2017) 1038–1043.
关于昊量光电:
上海昊量光电设备有限公司是光电产品专业代理商,产品包括各类激光器、光电调制器、光学测量设备、光学元件等,涉及应用涵盖了材料加工、光通讯、生物医疗、科学研究、国防、量子光学、生物显微、物联传感、激光制造等;可为客户提供完整的设备安装,培训,硬件开发,软件开发,系统集成等服务。
您可以通过我们昊量光电的官方网站www.auniontech.com了解更多的产品信息,或直接来电咨询4006-888-532。