

筑基:斯坦福 线性动力系统导论——矩阵运算
1矩阵运算
●置,和,差,数乘
●矩阵乘法,矩阵-向量积
●矩阵求逆
2矩阵转置(matrix transpose)
m X n的矩阵A的转置,记为AT或A’,A的转置矩阵大小为n X m

A的行和列都颠倒过来就是AT,例子:

●转置将行向量变成列向量,反之亦然
●(AT)T=A
3矩阵加法&矩阵减法
如果矩阵A和矩阵B大小都为m X n,A+B通过对应元素相加完成,例子:

矩阵减法类似:
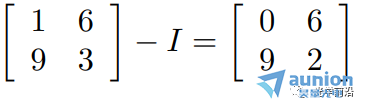
(注意,根据此处语义,单位矩阵I的大小为2 X 2)
4矩阵加法的特性
●交换律:A+B=B+A
●结合律:(A+B)+C=A+(B+C),所以可以写为A+B+C
●A+0=0+A=A;A-A=0
●(A+B)T=AT+BT
5纯量乘法(Scalar multiplication)
一个数(标量,或纯量)与一个矩阵相乘,通过这个数与矩阵内的每一个元素相乘完成
数乘将标量和矩阵毗邻表示或者用“·”连接表示:

●(α+β)A=αA+βA; (αβ)A=(α)(βA)
●α(A+B)=αA+αB
●0·A=0; 1·A=A
6矩阵乘法
如果A大小为m X p,B大小为p X n,则可令C=AB,C的大小为m X n
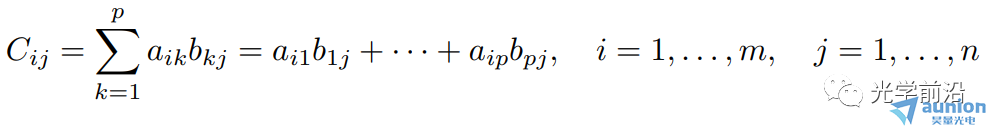
矩阵A和矩阵B能相乘的前提是A的列数必须等于B的行数
7例子
例1:

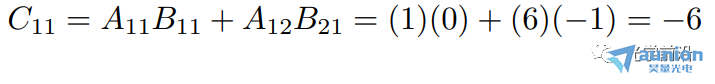
例2:
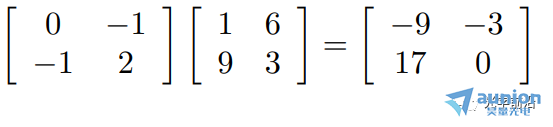
矩阵乘法一般是不可交换的,即AB一般不等于BA
8矩阵乘法的特性
●0A=0,A0=0(此处的0可以是标量,也可以是矩阵)
●IA=A,AI=A
●(AB)C=A(BC),也可写为ABC
●α(AB)=(αA)B,α是标量
●A(B+C)=AB+AC,(A+B)C=AC+BC
●(AB)T=BTAT
9矩阵-向量积
矩阵乘法非常重要的特例是:y=Ax
●A是m X n矩阵
●x是n-向量
●y是m-向量
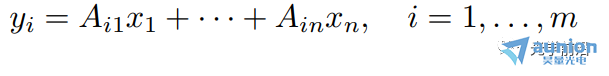
y=Ax可被认为是
●一个将n-向量转换为m-向量的函数
●一组将x和y联系起来的m个线性方程
10内积
当ν是含n个元素的行向量,ω是含n个元素的列向量时,νω就有意义,且是一个大小为1 X 1的标量:

元素数相同的向量x和y,xTy是标量,称为x和y的内积或点积,记为
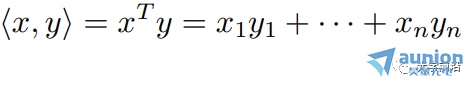
11矩阵幂
当矩阵A是方阵的时候,积AA有意义,通常记为A2,k个A相乘记为 Ak

按照惯例,A0=I
AkAl=Ak+l
12矩阵求逆
如果矩阵A是方阵,存在方阵F使得FA=I,则
●F称为A的逆,记为A-1
●矩阵A称为可逆的或非奇异的
如果A不存在逆,则称为奇异的或不可逆的
AA-1=I
A的负数幂定义为A-k=(A-1)k
13例子
例1:
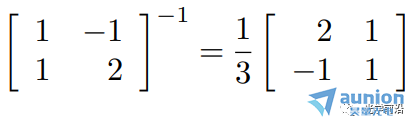
例2: 没有逆。假设其存在逆,则有
没有逆。假设其存在逆,则有

而满足a-2b=1和-a+2b=0的a,b无解
14逆的特性
●(A-1)-1=A,即逆的逆是原矩阵(假设A是可逆的)
●(AB)-1=B-1A-1(假设A和B都可逆)
●(AT)-1=(A-1)T(假设A是可逆的)
●I-1=I
●(αA)-1=(1/α)A-1(α≠0) (假设A是可逆的)
●如果y=Ax,x∈Rn,A是可逆的,则x=A-1y:
![]()
15 2 X 2矩阵的逆
知道2 X 2矩阵的逆的一般公式是有用的:
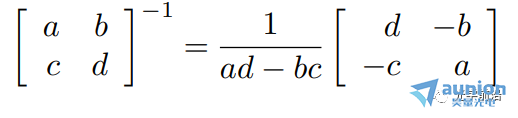
ad-bc≠0(如果ad-bc=0,则矩阵式奇异的)
参考文献:Introduction to Linear Dynamical Systems. Stephen Boyd
关于昊量光电:
上海昊量光电设备有限公司是国内知名光电产品专业代理商,代理品牌均处于相关领域的发展前沿;产品包括各类激光器、光电调制器、光学测量设备、精密光学元件等,涉及应用领域涵盖了材料加工、光通讯、生物医疗、科学研究、国防及更细分的前沿市场如量子光学、生物显微、物联传感、精密加工、先进激光制造等;可为客户提供完整的设备安装,培训,硬件开发,软件开发,系统集成等优质服务。
您可以通过昊量光电的官方网站www.auniontech.com了解更多的产品信息,或直接来电咨询4006-888-532。
本文章经光学前沿授权转载,商业转载请联系获得授权。
展示全部 