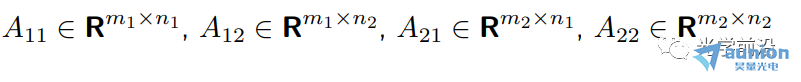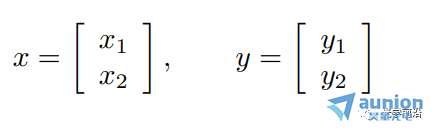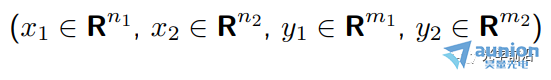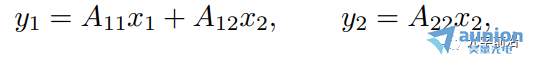Lecture 2
线性函数和例子
线性方程和函数
工程例子
解释
筑基:斯坦福 线性动力系统导论——第二课
1Lecture 2 线性函数和例子
●线性方程和函数
●工程例子
●解释
2线性方程
考虑一个线性方程描述的系统
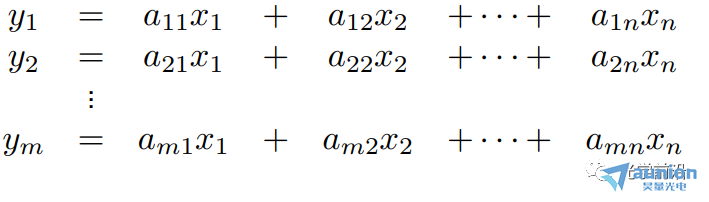
可以写成y=Ax的矩阵形式
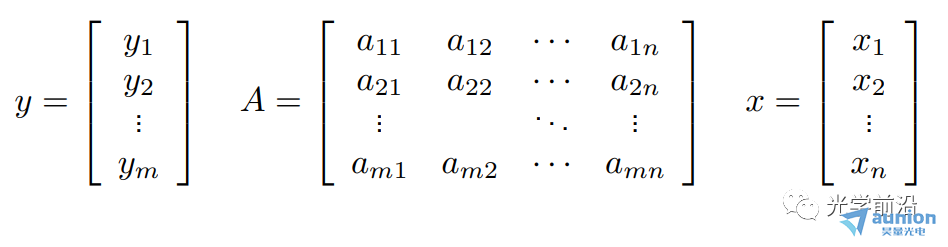
3线性函数
函数f : Rn → Rm是线性的,当
f(x + y) = f(x) + f(y), ∀x,y∈Rn
f(αx) = αf(x), ∀x∈Rn∀α∈R
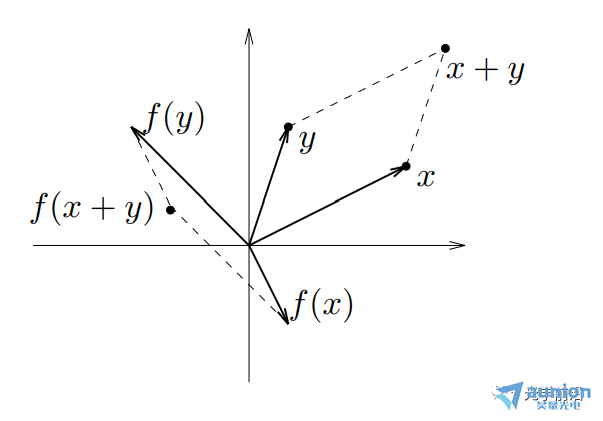
4矩阵乘法函数
●考虑函数f : Rn → Rm,f(x)=Ax,其中A∈Rm×n
●矩阵乘法函数是线性的
●逆命题也成立:任何线性函数f : Rn → Rm 可以写为
f(x) = Ax ,A∈Rm×n
●通过矩阵乘法唯一表示:对任意的线性函数f,对于所有的x满足f(x)=Ax,存在唯一的矩阵A
5y=Ax的解释
●y代表测量或观察,x是需要确定的未知
●x是输入或行为,y是输出或结果
●y=Ax定义了一个函数或变换,其将x∈Rn 映射到y∈Rm
9aij的解释

aij是从第j个输入(xj)到第i个输出(yi)的增益系数
所以,
●A的第i行涉及第i个输出
●A的第j列涉及第j个输入
●a27=0意味着第2个输出(y2)不取决于第7个输入(x7)
●|a31|>>|a3j|,当j≠1意味着y3仅仅取决于x1
●|a52|>>|ai2|,当i≠5,意味着x2主要影响y5
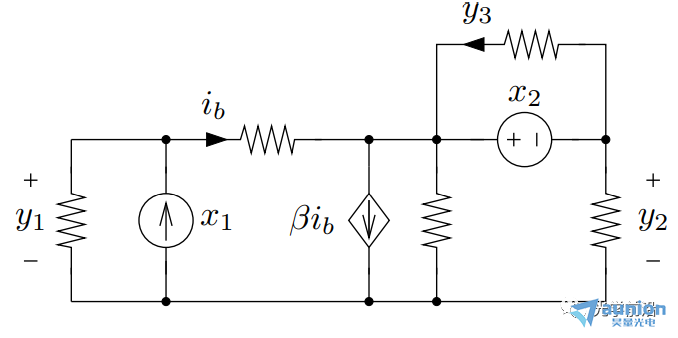
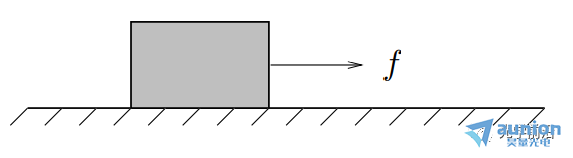
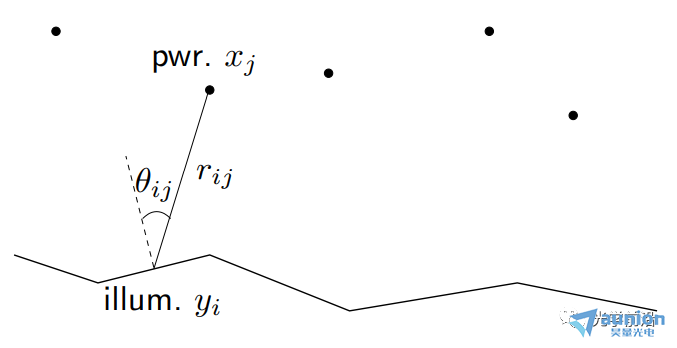
●当A是下三角矩阵,即当i ●当A是对角矩阵时,即i≠j时,aij=0,意味着第i个输出只取决于第i个输入 10线性弹性结构 ●xj是作用在某个节点上的外部施加力,方向固定 ●yi(很小)是某个节点在外部施加力下产生的挠曲,方向固定 (考虑到x,y都很小),可以得到y≈Ax ●aij给定了在j处每单位力(m/N)产生的挠曲i 11刚体上的合力/扭矩 ●xj是施加在某一点/方向/轴上的外部力/扭矩 ●y∈R6 是刚体上产生的合力&扭矩 (y1,y2,y3是x-,y-,z-分量的合力, y4,y5,y6是x-,y-,z-分量的合扭矩) ●有y=Ax ●A取决于几何形态(相对于重心CG施加的力和扭矩) ●第j列给出单位力/力矩的合力合扭矩 12线性静态电路 电阻、线性依赖(被控制的)源和独立源的连接 ●xj是第j个独立源 ●yi是一些电路变量(电压,电流) ●有y=Ax ●如果xj是电流,yi是电压,A则称为阻抗或电阻矩阵 13在外部力作用下物质的最终位置/速度 ●单位质量物质,在t=0的时候处于0位置/速度,在0≤t≤n受到力f(t) ●f(t)=xj,j-1≤t ●y1,y2是最终的位置和速度(在t=n时刻) ●有y=Ax ●a1j是在j-1≤t ●a2j是在j-1≤t 14热系统 ●xj是第j个加热元件或热源的功率 ●yi是位置i处稳态温度的变化 ●通过热传导完成热传输 ●y=Ax ●aij表示位置i处热源j的影响 ●A的第j列给出热源j在1W功率时稳态温度上升的模式 ●A的第i行表示各个热源对位置i的影响 15多个光源照明 ●n个光源照射m个小而平的块(patch),无阴影 ●xj是第个光源的功率,yi是第i个块的照明水平 ●y=Ax,aij=rij-2max{cosθij,0} (cosθij<0意味着第i个块与光源j之间是遮挡的) ●A的第j列描述光源j的照明模式 16无线系统中的信号和干扰功率 ●n个发射器/接收器对 ●发射器j向接收器i发送(并且不经意间发送到其它接收器) ●pj是第j个发射器的功率 ●si是第i个接收器接收到的信号功率 ●zi是第i个接收器接收到的干扰功率 ●Gij是从发射器j到接收器i的路径增益 ●有s=Ap,z=Bp,其中 17生产成本 生产投入(材料、零件、劳动力......)组合起来制造一系列产品 ●xj是每单位生产投入j的价格 ●aij是制造单位产品i所需要的生产投入j的单位量 ●yi是每单位产品i需要的生产成本 ●有y=Ax ●A的第i行是生产单位产品i所需的材料账单 生产所需投入 ●qi是要生产产品i的量 ●rj是生产所需输入j的总量 ●有 总生产成本为 18线性化 ●如果f : Rn → Rm,在x0∈Rn可微,则 x在x0附近⇒f(x)很接近f(x0)+Df(x0)(x-x0),其中 是导数(雅可比)矩阵 ●y=f(x),y0=f(x0),定义输入偏差(derivation)δx:=x-x0,输出偏差δy:=y-y0 ●有δy≈Df(x0)δx ●当偏差很小的时候,用一个线性函数将它们(δx和δy)近似联系起来 19通过距离测量来导航 ●(x,y)是平面上的未知坐标 ●(pi,qi)是已知的信标(beacons)坐标,i=1,2,3,4 ●ρi测量从信标i到未知点的距离 ●ρ∈R4是(x,y)∈R2的一个非线性函数: ●在(x0,y0)附近作线性化: 其中, ●A的第i行显示(x, y)从(x0, y0)的(小)偏移距离测量的(近似)变化 ●A的第一列表示距离测量对x从x0的(小)变化的敏感性 20广泛的应用类别 线性模型或函数y=Ax 一些更广泛的应用类别: ●估算或求逆 ●控制或设计 ●映射或变换 21估算或求逆 ●yi是第i个测量或传感器读取(已知的) ●xj是第j个需要估算或确定的参数 ●aij是第i个传感器对第j个参数的灵敏度 问题示例: ●给定y,确定x ●找到导致y的所有x ●如果没有x满足y=Ax,则,找到x满足y≈Ax 22控制或设计 ●x是设计参数向量或输入向量 ●y是结果向量或输出 ●A描述输入选择如何影响结果 问题示例: ●找到x,使得y=ydes ●找到导致y=ydes的所有x ●在满足y=ydes的x中,找到最小的那个 23映射或变换 ●x由线性函数y=Ax映射或变换到y 问题示例: ●确定是否存在x映射到给定的y ●(如果可能)找到映射到y的x ●找到映射到给定y的所有的x ●如果只有一个x映射到y,找到它(即解码或撤销映射) 24矩阵乘法作为列的混合 将A∈Rm×n写为列的组成: 其中aj∈Rm y=Ax可以写为 (xj是标量,aj是m向量) ●y是A的列的线性组合 25一个重要的例子:x=ej,第j个单位向量 那么Aej=aj,A的第j列 26矩阵乘法作为与行的内积 将A写为行向量混合的形式: 其中 那么y=Ax可以写为 即yi是A的第i行和x的内积 几何解释: 27框图表示 y=Ax可以用信号流图或框图表示 例:m=n=2,有 框图表示为 ●aij是从j输入到i输出的增益 例子:块上三角矩阵 x和y相应的分块 其中 从而 框图表示为: 即y2不取决于x1 参考文献:Introduction to Linear Dynamical Systems. Stephen Boyd 关于昊量光电: 上海昊量光电设备有限公司是国内知名光电产品专业代理商,代理品牌均处于相关领域的发展前沿;产品包括各类激光器、光电调制器、光学测量设备、精密光学元件等,涉及应用领域涵盖了材料加工、光通讯、生物医疗、科学研究、国防及更细分的前沿市场如量子光学、生物显微、物联传感、精密加工、先进激光制造等;可为客户提供完整的设备安装,培训,硬件开发,软件开发,系统集成等优质服务。 您可以通过昊量光电的官方网站www.auniontech.com了解更多的产品信息,或直接来电咨询4006-888-532。 本文章经光学前沿授权转载,商业转载请联系获得授权。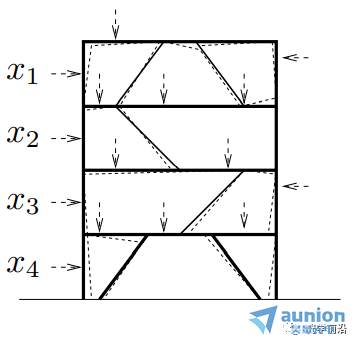




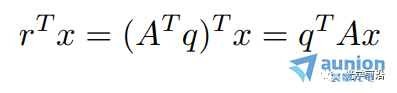
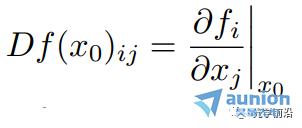

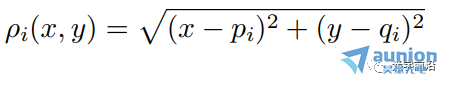
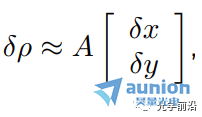


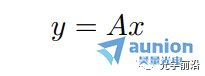


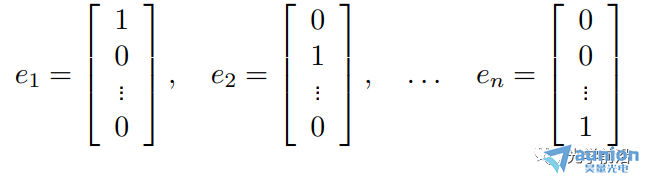



 是Rn上的一个超平面(垂直于对应列向量)
是Rn上的一个超平面(垂直于对应列向量)