筑基：斯坦福 线性动力系统导论——线性方程和矩阵

正文

筑基：斯坦福 线性动力系统导论——线性方程和矩阵

1线性方程和矩阵

●线性函数

●线性方程

●求解线性方程

2线性函数

函数f将n-向量映射到m-向量是线性的前提为：

●放缩(scaling):对任意n-向量x，任意放缩比α，有f(αx) = αf(x)

●叠加(superposition):对任意n-向量u和v,f(u + v) = f(u) + f(v)

例子：

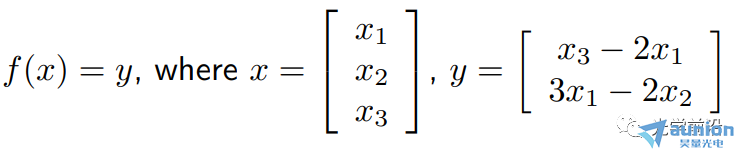
验证其缩放特性：

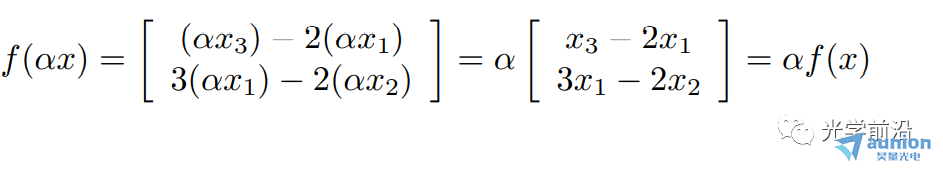
3矩阵乘法和线性函数

一般情形：f(x) = Ax,其中A是m X n矩阵

●放缩：f(αx) = A(αx) = αAx = αf(x)

●叠加：f(u + v) = A(u+v) = Au + Av = f(u) + f(v)

因此，矩阵乘法是一个线性函数

相反的，每一个线性函数y=f(x),其中y是一个m-向量，x是一个n-向量，可以表示成y=Ax，矩阵A大小为mXn

当x= ej的时候，可以从Aij=yi得到A的系数

4线性函数的组成

假设

m-向量是n-向量的一个线函数，即，y=Ax，其中A是mXn矩阵

p-向量z是y的一个线性函数，即z=By,其中B是pXm矩阵

则，z是x的一个线性函数，且z=By=(BA)x

所以矩阵乘法对应线性函数的组成，即某些变量的线性函数的线性函数

5线性方程

如果方程两边都由包含xi的倍数以及常数的和组成，那么关于变量x1,…,xn的方程是线性的，例：

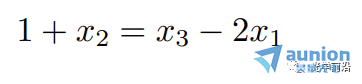
是关于x1,x2,x3的线性方程

任意关于变量x1,…,xn的m个线性方程的集合都可以由矩阵方程来表示

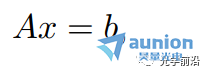
其中，A是一个m X n的矩阵，b是一个m-向量

6例子

关于3个变量x1,x2,x3的两个方程

步骤1：重写方程，让变量在左边，每个方程变量的顺序一致，没有的用0xn代替；常数项放在方程右边：

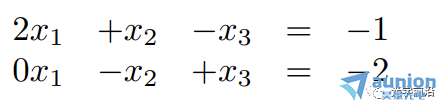
(每一行是一个方程)

7

步骤2：将方程重写为一个矩阵方程：

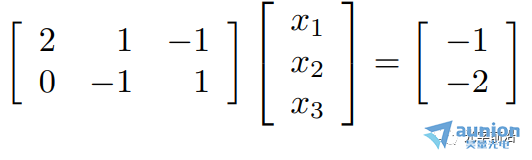
A的第i行是第i个方程的系数

A的第j列是方程的xj的系数

b的第i项是第i个方程的常数项

8求解线性方程

假设有n个变量x1,…,xn的n个方程，写成矩阵形式Ax=b,则A是一个n X n矩阵，b是一个n-向量

假设A是可逆的，即，它的逆A-1存在

在Ax=b两边同时左乘A-1:

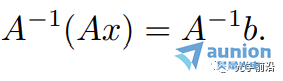
左边简化为

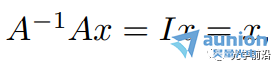
从而线性方程被求解为：

注意，手算求解x=A-1b是工作量相当大的，但是使用计算机就很快。

9当矩阵A不可逆，即A的逆不存在时

●一个或多个方程是冗余的（即这些冗余方程可以由其它的方程得到）

●方程组是前后矛盾或者相互矛盾的

实际上：A不可逆意味着我们构建了一个错误的方程组，或者方程数不够

10实际求解线性方程

在计算机上求解Ax=b(即，计算x=A-1b)，我们不计算A-1，然后将其与b相乘(当然这样做也是可以的)

实际操作是通过特殊的方法直接计算x=A-1b（在数值线性代数里研究）

用稀疏矩阵求解方程

在许多应用中A有许多或几乎所有的项是0，这时称其为稀疏的。计算机求解稀疏线性方程特别高效。

参考文献：Introduction to Linear Dynamical Systems. Stephen Boyd

关于昊量光电：

上海昊量光电设备有限公司是国内知名光电产品专业代理商，代理品牌均处于相关领域的发展前沿；产品包括各类激光器、光电调制器、光学测量设备、精密光学元件等，涉及应用领域涵盖了材料加工、光通讯、生物医疗、科学研究、国防及更细分的前沿市场如量子光学、生物显微、物联传感、精密加工、先进激光制造等；可为客户提供完整的设备安装，培训，硬件开发，软件开发，系统集成等优质服务。

您可以通过昊量光电的官方网站www.auniontech.com了解更多的产品信息，或直接来电咨询4006-888-532。

本文章经光学前沿授权转载,商业转载请联系获得授权。