在变形系统中的所有近轴量都可以用两个相关RSOS中四个已知的非偏斜近轴光线的跟踪数据以及物体和光阑变量来表示。
变形系统系列（十一）-变形系统的近轴像性质-第四部分
从之前的讨论中，我们知道，即使在一个变形系统中只有两条线性无关的近轴斜光线，而且任何其他的近轴光线都可以被书写为这两条光线的线性组合，实际上，使用四个单独已知的非斜近轴光线更方便——在x-z子午线平面上追踪的与x-RSOS相关的近轴边缘光线和主光线以及在y-z子午线平面上追迹的与y-RSOS相关的近轴边缘光线和主光线。
当我们处理任意变形近轴(倾斜或非倾斜)光线的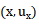
分量时，我们将使用位于变形系统的x-z对称平面上的x-边缘光线和x-主光线。类似地，当我们处理同一变形近轴光线的 
分量时，我们将使用停留在变形系统的y-z对称平面上的y-边缘光线和y-主光线。
让我们写 
作为x- rsos中x-边缘和y-主光线的相关参数，y同理，在j曲面上。我们可以得到
是整个系统的比例常数，可由任意变形近轴光线的初始条件求出。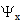
是与由虚拟球面
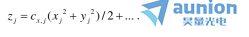构成的x-RSOS相关的x-拉格朗日不变量。 
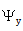同理。
现在我们求出比例常数的值
。假设任意变形近轴光线在
点切割近轴目标平面(j=0)。设
为该物体点到光轴的距离，设极坐标角为φ。然后遵循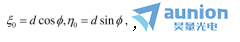
，如下图所示。假设最大孔径为 
，我们将量
定义为分数孔径(stop)。
由上式可知，在近轴目标平面(j=0)，有
在该平面中，x边缘射线高度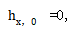 
, x-主光线高度
和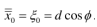
。我们能够得到
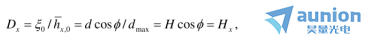
对于任意近轴光线，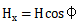
是分数场在变形系的x-z对称平面上的投影。
在系统的光阑面(j=p)，我们将有
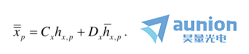
在这个平面中，x-边缘光线高度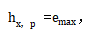
，x-主光线高度
。我们得到
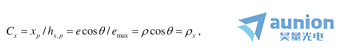
对于这条光线，这里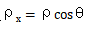
是分数孔径ρ在x-z对称平面上的投影。
因此，我们发现了比例常数，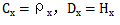
这是整个系统的常数。对于任意曲面j，之前的方程可变成
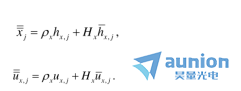
类似地，我们可以找到比例常数，
。对于任意曲面j，之前的方程可变成
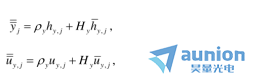
我们认识到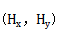
和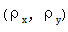
实际上是这个任意变形近轴光线的归一化对象和孔径坐标。
上四式将作为畸变系统畸变系数初始推导的基础。这些方程可以这样理解:
1）在变形系统中，任意变形近轴光线(倾斜或不倾斜)的光线追迹数据可以由两个相关RSOS中四个已知的不倾斜的近轴边缘和主光线追迹数据的线性组合而成。
2）此外，比例常数是所研究的任意变形近轴射线的归一化对象和光阑坐标。还要注意，当我们探索物体和光阑平面时，这些坐标是变量。
因此，变形系统中的所有近轴量都可以用两个相关RSOS中四个已知的非偏斜近轴光线的跟踪数据以及物体和光阑变量来表示。
相关文献：
《几何光学 像差 光学设计》（第三版）——李晓彤 岑兆丰
关于昊量光电：
上海昊量光电设备有限公司是光电产品专业代理商，产品包括各类激光器、光电调制器、光学测量设备、光学元件等，涉及应用涵盖了材料加工、光通讯、生物医疗、科学研究、国防、量子光学、生物显微、物联传感、激光制造等；可为客户提供完整的设备安装，培训，硬件开发，软件开发，系统集成等服务。
您可以通过我们昊量光电的官方网站www.auniontech.com了解更多的产品信息，或直接来电咨询4006-888-532。
展示全部 
