椭偏仪与偏振相位（四）-光强测量法的原理及误差分析

正文

椭偏仪与偏振相位（四）-光强测量法的原理及误差分析

光强测量法

1.测量原理

所谓光强测量法是通过测量测试系统透过的光强值，利用透过光强与待测元件位相延迟关系计算出待测元件延迟值。测试系统构成与光谱扫描法相同，系统出射光强表达式也相同。式中Ω和θ是两个zui活跃的量，容易改变并准确测量。因此理论上讲，为避开对的测量，可任意测定两组不同的Ω和θ的光强值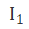及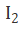，即可求出待测元件的延迟，其结果可以表示为：

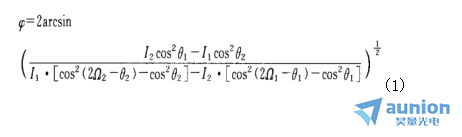
式(1)是光强法的通解。当保持θ不变，改变波片方位角Ω进行测量的方法为旋转待测波片法；而当保持Ω不变，改变θ的测量方法为旋转检偏器法。下面简述这两种常用方法的原理。

(1) 旋转待测波片法：

旋转波片法通常采用读取旋转过程中光强的zui大值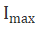和zui小值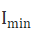的办法，从而可以避开对光轴方位角Ω的测量误差。对系统出射光强表达式分析可知，当Ω=θ/2时，系统光强取得zui大值；当Ω=θ/2+π/4时，光强取得zui小值，则波片的位相延迟φ可表示如下：

其中，θ≠90°。

(2)旋转检偏器的方法：

旋转检偏器的方法通常取Ω=45°，θ分别取0°和90°，因为误差分析表明此时由角度测量造成的误差zui小(详见误差分析)。分别记录θ=0°和90。时的光强为及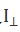，则波片的位相延迟φ可表示为：

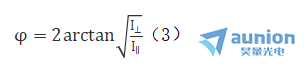
这两种测试方法的优点是便于实现计算机控制和数据的采集及处理，测试速度快。采用多次测量及曲线拟合等办法可以有效降低光源波动和其它偶然误差的影响。

2.误差分析

(1)各参量测量误差对测量结果的影响：

分析各参量误差对测量结果的影响可以从式(1)出发，分别考察当各量存在微小变化时得到的延迟测量结果与理论结果相对照，并以二者差值来表示各量误差对测量结果的影响。由公式可见，各项误差比较复杂不但与各个参量的取值有关，而且与待测波片的延迟φ有关，因此这里仅针对常用的λ／4与λ／2波片，分析式(2)和式(3)两种方法的误差。代入测试系统的精度，转台精度Δθ，△Ω≤1′光源强度波动为△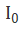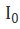／≤0．14%，由此得出误差分析结果列表如下：

                                        旋转波片法的误差

波片	θ（°）	影响（%）	影响（%）	θ影响（%）	综合误差（%）
λ/4	0	0.089	0.089	0.000003	0.18
	45	0.037	0.067	0.019	0.14
λ/2 *	0	0	0	0	0
	45	0	0	0	0

*表示实验条件下各参量测量误差对λ／2波片测量结果影响很小，说明该项影响不是误差主要来源。

                                         旋转检偏器法的误差

波片	影响（%）	影响（%）	影响（%）	影响（%）	Ω影响（%）	综合误差（%）
λ/4	0.045	0.045	0	0	0.00003	0.064
λ/2	0	0	0	0.019	0.037	0.042

 

(2)带宽对测量的影响：

实测光强值可表示为：

而式(1)虽然是在理想情况下得到的，但可以将光强测量值理解为I′≈i(λ)·Δλ。因此，误差可以表示为：

仍以实测情况为例，在中心波长λ=637.8nm处，带宽对λ／4波片误差＜0.0005%；对λ／2波片误差＜0.07%。可见实验条件下带宽对测量的影响很小。

(3)偏振器的消光比对测量的影响：

当考虑偏振器的消光比时，系统透过光强的表达式非常复杂。仅以式(2)为例，当θ=0°时，系统透过光强zui大值则可近似表示为：

若以φ(0)表示理想偏振器的测量值，φ(a)表示考虑消光比的测量值，则误差可以按下式估算：

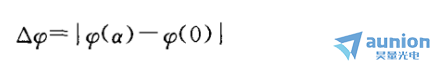
若按a≈10^-5计算，对旋转波片法而言，当θ=0°时，λ／4波片误差＜0.002%，λ／2误差＜0.29%；当θ=45°时，λ／4波片误差＜0.2%，6，λ／2误差＜0.45%。对旋转检偏器法而言，λ／4波片误差很小可以忽略，λ／2误差＜0.29%。

(4)其它误差

综合考虑上述各项误差，不难发现测量误差zui大者也仅仅为0.46%，但从之前的测量数据看，实测差异远远大于上述分析结果。上述分析证明，上述各项误差不足以造成较大的测量差异，因而仅考虑上述测量误差对光强法还远不够全面。这是因为与光谱法和Soleil补偿器法不同，光强法需要读取绝对光强值，而诸如杂散光、光路的缺陷和光学元件的缺陷等许多复杂因素zui终都将反映在光强测量值中，从而影响测量结果。由于这些误差非常复杂，这里仅做定性描述：

(a)由测量方法缺陷带来的误差。测量λ／2波片时，由待测波片自身带来的杂散光、仪器本底等原因使得光强的zui小值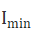和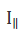》O，因而代入式(2)、（3)计算时将无法得到180°延迟量；

(b)Glan棱镜应用于扩展光束光路中会导致消光比的损失；

(c)Glan棱镜的制造缺陷通常会带来3～6分的光束偏离，若扩展光束光强分布不均匀(例如灯丝像分布)，那么在旋转检偏器的时候会出现严重的问题。由之前测量结果可见，此类误差对旋转检偏器的方法测量会造成巨大的影响。

综合上述分析可见，实验条件下各参量测量误差及带宽影响不是影响测量精度的主要因素，测量误差主要来源于Glan棱镜的光束偏离及其应用于扩展光束中的消光比损失等造成的影响。由此可见，光强法对光路及光学元件等要求较高，在本文所采用实验系统中难以获得较高的测量精度。

 

了解更多详情，请访问上海昊量光电的官方网页：

https://www.auniontech.com/three-level-56.html

相关文献：

1王勇辉,郑春龙,赵振堂.基于斯托克斯椭偏测量系统的多点定标法[J].中国激光,2012,39(11):163-167.

2侯俊峰,于佳,王东光,邓元勇,张志勇,孙英姿.自校准法测量波片相位延迟[J].中国激光,2012,39(4):173-179. 

3王喜宝,宋连科,朱化凤,郝殿中,蔡君古.连续偏光干涉法测量波片宽波段延迟量变化[J].激光技术,2012,36(2):258-261. 

4赵振堂,林天夏,黄佐华,何振江.利用消光式椭偏仪精确测量波片相位延迟量[J].激光杂志,2012,33(3):8-9.

5程一斌,侯俊峰,王东光.组合波片的椭圆率角测量方法[J].北京理工大学学报,2019,39(7):750-755. 

6于德洪,李国华,苏美开,宋连科.任意波长云母波片位相延迟的测量[J].光电子．激光,1990,1(5):267-269.

7徐文东,李锡善.波片相位延迟量精密测量新方法[J].光学学报,1994,14(10):1096-1101. 

8薛庆文,李国华.半阴法测量λ/4波片的相位延迟[J].光电子．激光,1998,9(2):150-151.

9 AzzamR. M. A., Bashara, N. M. ellipsometry and Polarized Light[M]. New York: North - Holland, 1977,198 - 201.

10孙英姿,王东光,张志勇,邓元勇,张洪起,玄伟佳.波片相位延迟的光强测量法研究[J].天文研究与技术,2008,5(1):74-82. 

更多详情请联系昊量光电/欢迎直接联系昊量光电

关于昊量光电：

上海昊量光电设备有限公司是光电产品专业代理商，产品包括各类激光器、光电调制器、光学测量设备、光学元件等，涉及应用涵盖了材料加工、光通讯、生物医疗、科学研究、国防、量子光学、生物显微、物联传感、激光制造等；可为客户提供完整的设备安装，培训，硬件开发，软件开发，系统集成等服务。

您可以通过我们昊量光电的官方网站www.auniontech.com了解更多的产品信息，或直接来电咨询4006-888-532。