稳定腔激光器发出的激光束是一种具有特殊结构的高单色性的高斯光束，它具有最小横向发散角，在光学元件边缘的衍射损耗最小。此外，高斯光束通过自由空间的传播和通过无像差透镜的变换时，除轮廓比例因子外，将始终保持高斯型分布。我们将首先介绍高斯光束的性质，然后讨论激光通过薄透镜后的性质变化，最后介绍激光扩束镜。
高斯光束及通过薄透镜时的变换及激光扩束镜（一）
高斯光束的基本性质
稳定腔激光器发出的激光束是一种具有特殊结构的高单色性的高斯光束，它具有最小横向发散角，在光学元件边缘的衍射损耗最小。此外，高斯光束通过自由空间的传播和通过无像差透镜的变换时，除轮廓比例因子外，将始终保持高斯型分布。
电矢量沿z轴方向传播的高斯光束的性质可以由下面三个方程式来决定：
上式中，R(Z)是距离坐标原点（束腰）Z处的高斯光束的波阵面的曲率半径（为球面），A(r)是高斯光束电矢量在r方向（也就是垂直于光波传播方向）的振幅，A0是波阵面中心的振幅，ω为光束的光斑半径，其中
分析式1可以知道，当Z 趋于0的时候，R(Z)趋于无穷，即此时波阵面为平面；当0≤|Z|≤ZR的时候，R(Z)逐渐减小，并且R(Z)>Z，即波阵面的曲率中心不在原点并且会随Z变化而变化，如下图所示。当Z= ±ZR时，ZR取到极小值±2ZR；而当Z ≫±ZR时，R(Z)重新增大，当Z趋于无穷的时候，变成平面波。
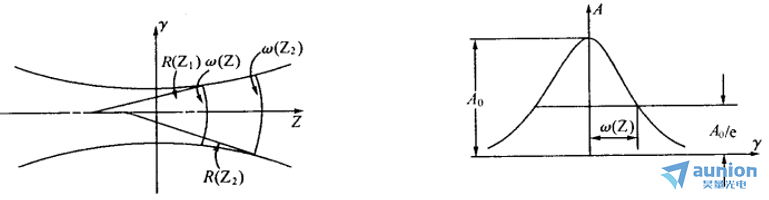
分析式2可以知道，高斯光束电矢量的振幅随高斯函数变化，在光束中心（r = 0）的地方振幅最大，如上图所示，所以高斯光束的光斑没有清晰的轮廓。式3中的光斑半径是振幅为A0/e，它又是Z的函数，如上图所示，当Z = 0 的时候，ω(0)= ω0为最小，它是高斯光束的束腰，ω0称为腰粗，Z ≫ZR的时候，有
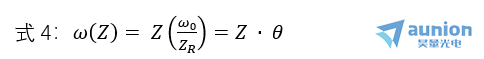
上式中，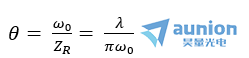
是高斯光束的远场发散角，用来描述高斯光束的发散角。2ZR为高斯光束的准直区，在这个范围内，高斯光束的光斑半径变化缓慢，准直性较好。在准直区的两端，Z= ZR，有ω= √2 ω0，光斑半径仅为束腰半径的√2倍。当Z ≫±ZR，为高斯光束的远场区，与普通球面波的变化规律完全相同。所以，普通球面波可以看作束腰半径ω_0=0的高斯光束。
所以，对于一个确定波长的高斯光束，当ω0一定的时候，R(Z)、ω(Z)、θ(Z)都可以确定，所以腰粗ω0是高斯光束的一个主要特征参量。
由于光束参数R(Z)、ω(Z)完全确定了高斯光束的几何形状，为了讨论方便，引入复曲率半径q(Z)，即
当Z = 0时，R(0)→∞，于是
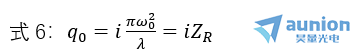
将式1、式3和式6代入式5得到
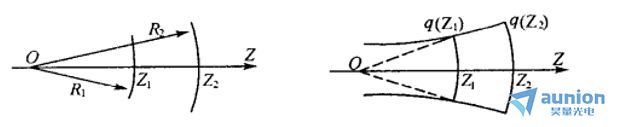
由此可见，q在高斯光束传播中的作用与球面波的曲率半径在球面波的传播中的作用一样，如上图所示，这表明，激光束是电磁波中光波段的一种新的传播形式，它的传播具有普遍的规律性，可以将普通球面波的传播规律认为是激光束的一种特殊情况。
相关文献：《几何光学 像差 光学设计》（第三版）——李晓彤 岑兆丰
您可以通过我们昊量光电的官方网站www.auniontech.com了解更多的产品信息，或直接来电咨询4006-888-532，我们将竭诚为您服务。
展示全部 
