高斯光束可以看作是均匀球面波的一种推广，博伊德和戈登理论已经证明：高斯光束传播轴线与透镜主轴重合的时候，通过透镜后仍为高斯光束。而对于薄透镜，透镜两侧的光斑尺寸相等，换言之，透镜两侧高斯光束的ω'= ω。本篇主要讲述高斯光束经透镜变换与几何光学中牛顿公式的关系，如果相同，此时可以使用几何光学的近轴公式使高斯光束的计算大为简化。我们将首先介绍高斯光束的性质，然后讨论激光通过薄透镜后的性质变化，最后介绍激光扩束镜。
高斯光束及通过薄透镜时的变换及激光扩束镜（三）
高斯光束可以看作是均匀球面波的一种推广，博伊德和戈登理论已经证明：高斯光束传播轴线与透镜主轴重合的时候，通过透镜后仍为高斯光束。而对于薄透镜，透镜两侧的光斑尺寸相等，换言之，透镜两侧高斯光束的ω'= ω。本篇主要讲述高斯光束经透镜变换的公式，以及如何设计一个良好的激光扩束镜，从而获得理想的准直效果。
当已知变换前后高斯光束束腰半径之比及变换透镜的焦距f'，则可用下列两式分别求得入射光束和出射光束的束腰到变换透镜的距离
其中由高斯光束通过薄透镜时的变换（二）可知，
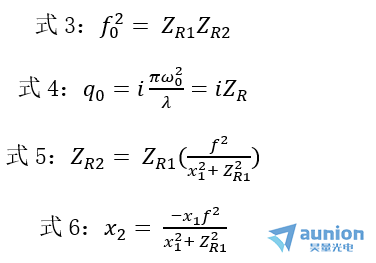
由此可见，变换透镜的焦距f'必须大于f0，否则无解。
若系统由多个透镜组成，上述公式对每个透镜都是适用的，透镜间的过渡公式为：
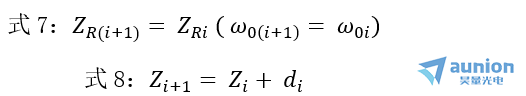
上面两式中Z, d的值都是相对于主面来说的。
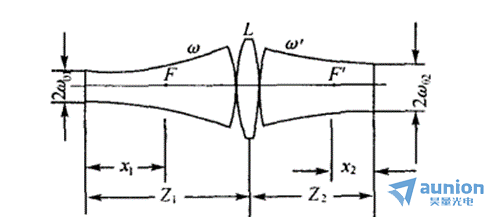
由式4和式5可知，ZR2的大小随x_1的增大而单调减小，当x1 → ∞时，由式6可知，x2 → 0，即出射高斯光束的束腰位于透镜焦点附近，这就是聚焦后光斑的大小。另外，高斯光束通过薄透镜时的变换（一）中提到过，电矢量沿z轴方向传播的高斯光束的性质可以由下面三个方程式来决定：
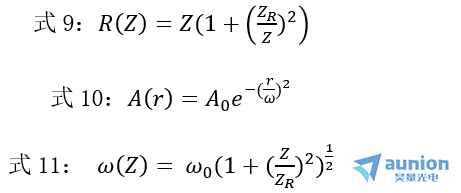
R(Z)是距离坐标原点（束腰）Z处的高斯光束的波阵面的曲率半径（为球面），A(r)是高斯光束电矢量在r方向（也就是垂直于光波传播方向）的振幅，A0是波阵面中心的振幅，ω为光束的光斑半径，其中
将式11平方除以式9可得光斑大小与R和Z的关系：
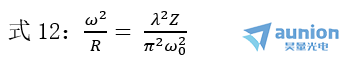
若出射光束的Z2 ≫ ZR2（远场），即R2= Z2 ≈ -f'，则
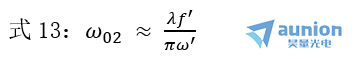
由式13可知，为了将高斯光束良好地聚焦，通常采用短焦距透镜，而且入射的高斯光束束腰远离透镜。聚焦后的光斑的大小可以由式13算出，为
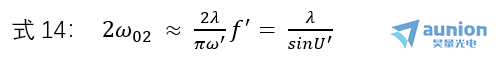
上式中
可见，焦斑尺寸相当于衍射斑直径，系统孔径角越大，焦斑尺寸越小，功率密度越高。
另一方面，当入射束腰位于透镜物方焦面时，即x1=0，由式6得x2=0,Z2= -f^'，如上右图所示。出射光束束腰也位于后焦面上。由式5得
于是
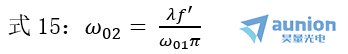
为极大值。可见，入射光束的束腰距离透镜焦点越近，出射光束的光斑直径越大。与前面比较可以知道，入射光束的束腰在无穷远或位于透镜的前焦点时，出射光束的束腰均位于像方焦点处，但光斑直径不同，前者为极小，后者为极大，即后者出射光束的远场发散角为极小，而且
据此，透镜的焦距f'越长，入射光束束腰ω01越小，则θ'越小，且当 ZR1 ≪ f'时，可使θ'小到可以忽略的程度。因此，常用的激光准直系统总是预先用一个短焦距透镜将高斯光束聚焦，以便获得极小的腰粗，然后用一个长焦距透镜来改善其方向性，就可以获得很好的准直效果。该系统即为倒置的伽利略望远镜或开普勒望远镜，称为激光扩束望远镜。
相关文献：《几何光学 像差 光学设计》（第三版）——李晓彤 岑兆丰
您可以通过我们昊量光电的官方网站www.auniontech.com了解更多的产品信息，或直接来电咨询4006-888-532，我们将竭诚为您服务。
