

高斯光束可以看作是均匀球面波的一种推广,博伊德和戈登理论已经证明:高斯光束传播轴线与透镜主轴重合的时候,通过透镜后仍为高斯光束。而对于薄透镜,透镜两侧的光斑尺寸相等,换言之,透镜两侧高斯光束的ω^'= ω。本篇主要讲述高斯光束经透镜变换与几何光学中牛顿公式的关系,如果相同,此时可以使用几何光学的近轴公式使高斯光束的计算大为简化。我们将首先介绍高斯光束的性质,然后讨论激光通过薄透镜后的性质变化,最后介绍激光扩束镜。
高斯光束及通过薄透镜时的变换及激光扩束镜(二)
高斯光束可以看作是均匀球面波的一种推广,博伊德和戈登理论已经证明:高斯光束传播轴线与透镜主轴重合的时候,通过透镜后仍为高斯光束。而对于薄透镜,透镜两侧的光斑尺寸相等,换言之,透镜两侧高斯光束的ω'= ω。本篇主要讲述高斯光束经透镜变换与几何光学中牛顿公式的关系,如果相同,此时可以使用几何光学的近轴公式使高斯光束的计算大为简化。
对于焦距为f'的薄透镜,薄透镜的成像公式为

高斯光束的复曲率半径表达式为

如下图所示,由物点0发出的球面波到达透镜左方的曲率半径为R1,通过透镜L的变换,在它右方出射的是曲率半径为R2的会聚球面波。并规定发散球面波的曲率半径为正,会聚球面波的曲率半径为负。
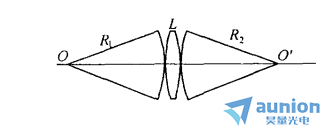
下图中设束腰半径为ω01的高斯光束的束腰与透镜的距离为Z1,通过透镜后像方高斯光束的束腰半径为ω02,与透镜距离为Z2,并令R1和R2分别为入射于透镜的波阵面半径和自透镜出射的波阵面半径,那么R1和R2应满足式1,必须注意的是,对于高斯光束,在一般情况下,R1 ≠ Z1,R2 ≠ Z2,只有在远场区域,才有R=Z的关系。
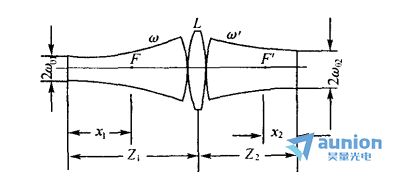
由式1、式2结合ω01=ω01得到
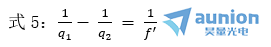
这时q1、q2分别为入射、出射高斯光束的复参量,可以由式3和式4写出它们的表达式。并将写出的表达式代入到式5,并使方程两边实部和虚部分别相等,再注意到图中关系f'- Z1= x1和f'+ Z2= -X2,得到
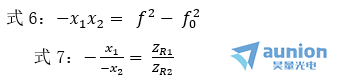
式6中f02= ZR1 ZR2
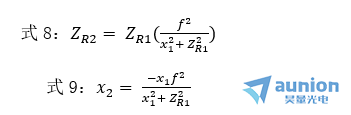
由式8和式9可以由物方束腰的1位置和大小求得像方束腰的位置和大小。由式6可见,当f0=0时,高斯光束经透镜的变换与几何光学中的牛顿公式一致,从而使高斯光束的计算大为简化,所以,下面三种情况可以使用几何光学的近轴公式:
ZR1 →0 即 ω01 →0
f' →0(如望远镜系统),此时f02可略去不计
x1 → ∞(远场)时
若以上条件不满足,则几何光学的近轴公式不适用。
相关文献:《几何光学 像差 光学设计》(第三版)——李晓彤 岑兆丰
您可以通过我们昊量光电的官方网站www.auniontech.com了解更多的产品信息,或直接来电咨询4006-888-532,我们将竭诚为您服务。
展示全部 
