绝大多数实际光学系统的成像是不完善的，像差就是不完善之处的具体表述。像差的种类多，描述复杂，我们不仅仅要从像差的几何意
义和表现特点入手，我们还要从像差的理论上深入研究，明确像差的表达式和计算。
一、球差的初步计算
球差也叫球面像差，Spherical Abereation，是所有几何像差中最简单也是最基本的像差，其中好几种轴外单色像差均与球差有一定联
系。不同倾角的光线交光轴于不同位置上，相对于理想像点的位置有不同的偏离。这是单色光的成像缺陷之一，称为球差。
如图所示
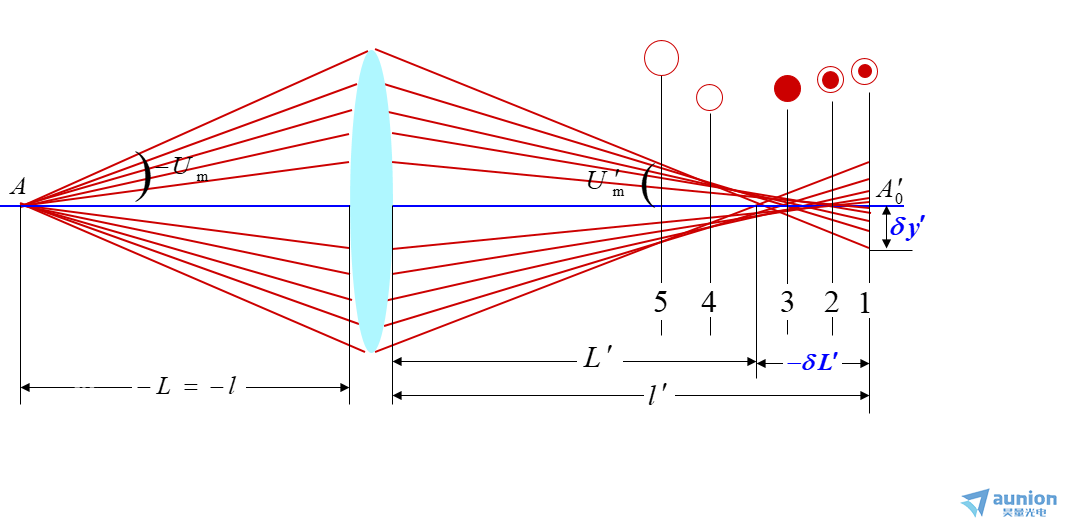
在上图中，在轴上点A的理想像为A0’,由A点发出的过入瞳边缘的光线（marginal ray)从系统出射后，交光轴于一点，而由于球差可
见到在12345个孔径带上成像不同，而它们的像方截距分别为L’于l’，则
其为这条光纤的球差。。显然，在边缘光纤以内与光轴成不同角度的各条光线都有各自的球差。
而如上图所示为球差小于0的情况。如果经过计算，使某一孔径带球差等于0，称为光学系统对这一环带光纤校正球差。大部分光学系
统只能对一环带光线校正球差，一般是对边缘光线校正的。这种光学系统叫消球差系统。
球差对成像质量的危害，是它在理想平面上引起半径为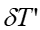
的弥散圆。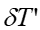 
称为垂轴球差，它与轴向球差
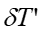之间有如下关系：
由于各环带的光线都有各自的球差，当轴上物点发出的充满人瞳的一束光通过光学系统后，这束光的各环带光线不能交于同一点，在像
面上将得到圆形的弥散斑，并且近轴像的位置并不一定是最小弥散圆的位置，可以将实际像面在近轴像的位置前后移动，找到对轴上点
成像的最佳像面。图上所示的12345孔径带的即为一光学系统在像面前后一段距离内的轴上点成像弥散斑。
轴上点以单色光成像时只有球差，但轴上点以近轴细光束所成的像是理想的，可见,轴上点球差完全是由于光束的孔径角增大而引起
的。所以，大孔径系统只允许有足够小的球差。同时由此还可看出，球差必然是U1或h1的函数。尽管它们之间的关系难以用显函数形
式表示出来，但由于光束的轴对称性质，可以简单地把球差表示成U1或h1的幂级数。考虑到当U1或h1变号时球差不变，以及当U1或
h1为零时球差为零，可写出以下两个表达式：
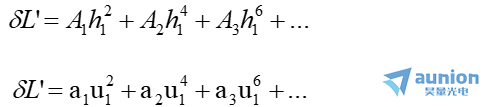
同理并结合上述轴向球差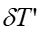
的公式考虑，得垂轴球差为
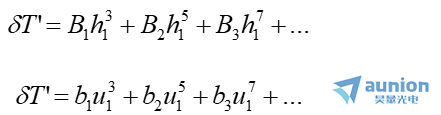
展开式中的第一项称为初级球差（primary spherical aberratiom），此后各项分别称为二级球差、三级球差等。二级以上的球差统称
为高级球差。
展示全部 
展示全部
