我们把波像差大致分为两类，一种是轴上点的波像差，另一种是轴外点的波像差，两者的影响因素以及与其相关的像差是不同的。此次我们分析的轴外点的波像差及其与垂轴像差之间的关系。
波像差系列（三）-轴外点的波像差及其与垂轴像差的关系
轴外点光束经光学系统后，一般已失去轴对称性质。因此不能像轴上点那样，仅用一个量来描述其像差。通常用光线的垂轴像差的子午分量
和弧矢分量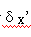
来描述，相应地,轴外点的波像差也将表示成与这两个分量之间的关系。
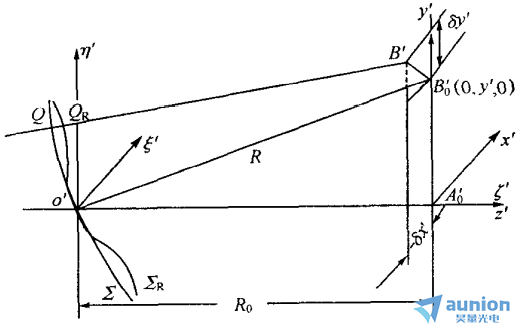
分别以出瞳中心o’和理想像面中心
为原点,作瞳面坐标
和像面坐标
如上图所示。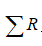
为轴外点B的实际波面，
为以理想像点
为中心所作的在出瞳中心o’处与实际波面相切或相交的理想参考球面。任取一条光线，与波面
,
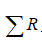和高斯像面分别相交于
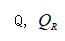和B'点,其坐标分别为
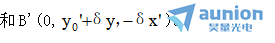光线的方向余弦为cosα，cosβ，cosγ。显然，
则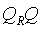
在三个坐标轴上的投影可以写成：
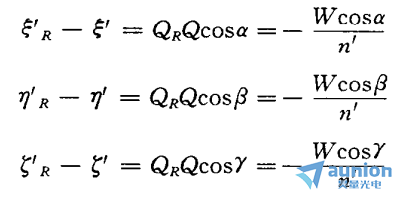
微分这些式子，并将第①式乘cosa,第②式乘cosβ,第③式乘cosγ,然后相加，考虑到方向余弦的平方和等于1,得
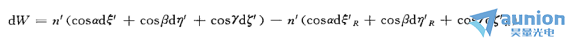
为进一步简化上式,对实际波面方程微分
，并考虑到实际波面上
点的法线即为光线，有
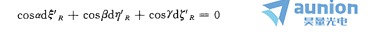
再根据上图，写出光线QB’的方向余弦，并令QB’=R。再写出理想参考球面方程式
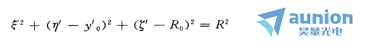
根据这些关系，Z终可将dW表达式写成为：
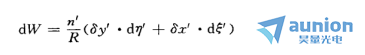
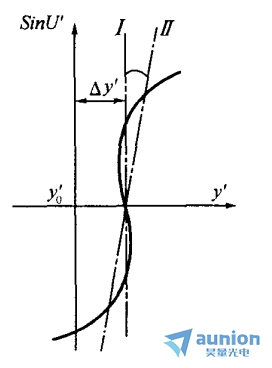
这就是轴外点波像差与垂轴几何像差之间的关系式。利用它可由几何像差求知波像差。反之亦然。为从光线的垂轴像差计算波像差,可对上面的公式进行积分。但是这样计算是相当不便的，因为要精确地把垂轴像差的二个分量表示成瞳面坐标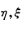
的函数关系非常复杂。因此，一般只利用这种关系分析和研究波像差与几何像差的关系。
通常,波像差是直接计算光线光程求得的。不过波面上沿子午截线的波像差还是容易在光学设计时从所算得的几何像差来判定。
上图所示为轴外点任一子午光线，与出瞳面的交点Q的坐标为
,与高斯像面的交点 高度为y’。距离 QB可认为等于参考球面的半径R,则有
将其微分的结果代入我们之前的到的式子，由于不涉及x'坐标,积分得
所以，只要计算出对应于各U’的光线与高斯像面的交点高度y’，画出
曲线，并使它通过
点,就得到
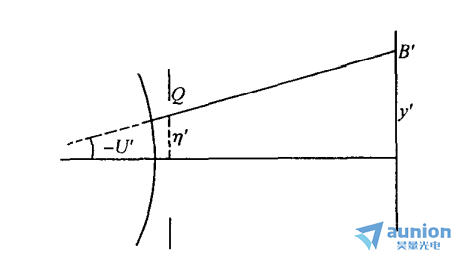
曲线，如下图 所示。这一曲线对 sinU’ 轴所围的面积，即为波面上沿子午截线的波像差。
上图中曲线与sinU'轴所围的面积，是以高斯像面上理想像点为参考点时的波像差，显然是比较大的。这也说明，当轴外点所成像有像差时,高斯像点也非较佳焦点所在。同样，可用离焦方法来寻求较佳参考点位置，以使波像差有所减小。不过对轴外点,离焦可在垂轴和沿轴两个方向进行。
先看垂轴离焦的情况。当参考点相对于高斯像点在垂轴方向作一微小移动时，相当于各条光线的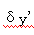
值改变了同样一个移动量，即纵坐标轴作了一个平移。从图中显而易见，纵轴移动Δy’至位置I时,波差将大为减小，所以，只要平移
曲线的纵轴，使其被曲线所包围的面积为小即可。垂轴离焦的目的，只是为了获知较佳参考点位置后，估计波像差大小以判断该像点的像质是否良好。
相关文献：
《几何光学 像差 光学设计》（第三版）——李晓彤 岑兆丰
关于昊量光电：
上海昊量光电设备有限公司是光电产品专业代理商，产品包括各类激光器、光电调制器、光学测量设备、光学元件等，涉及应用涵盖了材料加工、光通讯、生物医疗、科学研究、国防、量子光学、生物显微、物联传感、激光制造等；可为客户提供完整的设备安装，培训，硬件开发，软件开发，系统集成等服务。
您可以通过我们昊量光电的官方网站www.auniontech.com了解更多的产品信息，或直接来电咨询4006-888-532。
展示全部 
展示全部
