

如果一个光学系统的视场较小,其边缘点可认为与轴上点很靠近,这种近轴物点的像差性质要比远轴点简单得多。当光学系统对轴上点成完善像时,使在垂轴方向上与之无限靠近的物点也成完善像的充分必要条件称为正弦条件 (sine condition)。这就是说,若光学系统满足正弦条件,就能对小视场物面完善成像。正弦条件可由费马原理导出。
像差理论与计算系列(四)正弦条件
一、正弦条件的公式推导
如下图,光轴上的点 A 成完善像于A’。点B是在过点A 的垂轴方向上无限靠近A 的一点,设它也被系统成完善像于 B'。分别以y和y'表示AB 和A'B’。过A点的光线OA 与光轴成U 角,其共轭光线 O'A’与光轴成U’角。
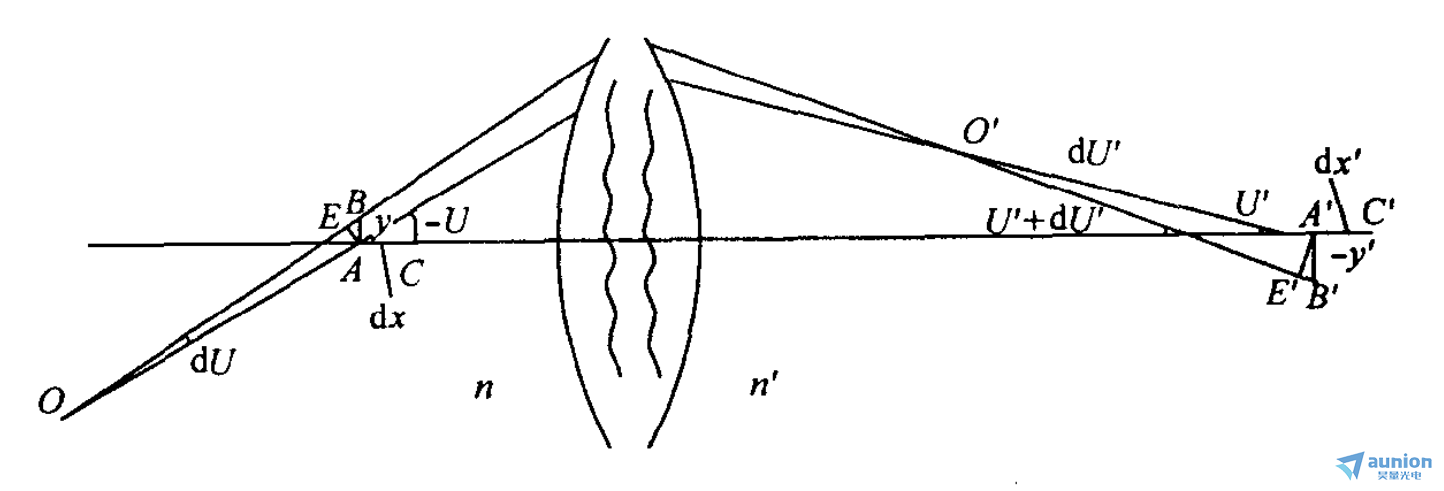
过B点的光线0B 与光轴成 U+dU 角,其共轭光线0'B'与光轴成 U’+ dU’角。根据费马原理,光程(OAA’0’)应与(OBB’0’)相等,即
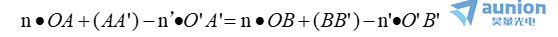
故有
 (a)
(a)
以O点为中心,OA为半径做圆弧,交光线OB于点E。因dU极小,从∆ABE可得
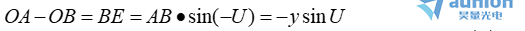 (b)
(b)
同理,在像方可得
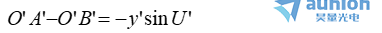 (c)
(c)
将(b)和(c)带入公式(a),得
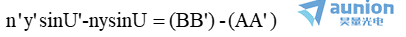
因A’和B’分别是A和B的完善像,根据费马原理,其间的光程各为极值,即
δ(AA’)=δ(BB’)=0,因此光程(AA’)和(BB')各为常数,二者之差也为常数,该常数可用一条沿光轴的光线来确定。对于这条光线,U=U'=0,故该常数为0,由此得
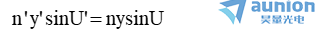
这就是正弦条件。这是光学系统对垂轴小面积成完善像所需满足的条件。或者说,当轴上点能以宽光束成完善像时,若满足此条件,过该点的垂轴小面积上的其他店也能以宽光束成完善像。
所以上述公式由可化为

当物体位于无穷远时,sinU=0,正弦条件须表示成另一种形式。以-(l-f)/f代替β,并有lsinU=h,可导出

显然,仅由轴上点光线的光路计算结果就能方便地判断光学系统是否满足正弦条件。例如边缘光线,若已对其校正了球差,并根据其光路计算结果求取比值 nsinU/n' sinU'或h/sinU',它们与按近轴光线所算得的放大率β=nu/nu'或焦距f’=h/u'之差为

即表示系统偏离正弦条件的程度。
二、等晕条件
光轴上校正了球差并满足正弦条件的一对共轭点,称为齐明点或不晕点。单个折射球面存在三对无球差的共轭点,其中l=l’=0和l=l’=r这二对显然满足正弦条件,而由l’=(n+n’)r/n’和l=(n+n’)r/n这一对,可得
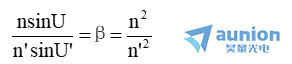
所以,以上三对共轭点都是满足正弦条件的齐明点。
正弦条件以轴上点完善成像为前提。但从球差的讨论可知,实际的光学系统仅能对物点发出的光束中的一个带或二个带的光线校正球差,因此,即使是轴上点也不可能是真正的完善成像。此外,轴上点球差校正不佳或不能校正时,成像也不完善。此时,轴外近轴点当然也不可能完善成像,充其量只能要求它的像质与轴上点一致,即具有相同程度的成像缺陷,我们称之为等晕成像 (aplanatic image formation)。
既然轴上点成像时只有球差,那么,根据等晕成像的要求,在垂轴平面上与之无限靠近的轴外点也只有球差,并且对应孔径角球差相等,二者具有相同的光束结构,如下图所示。
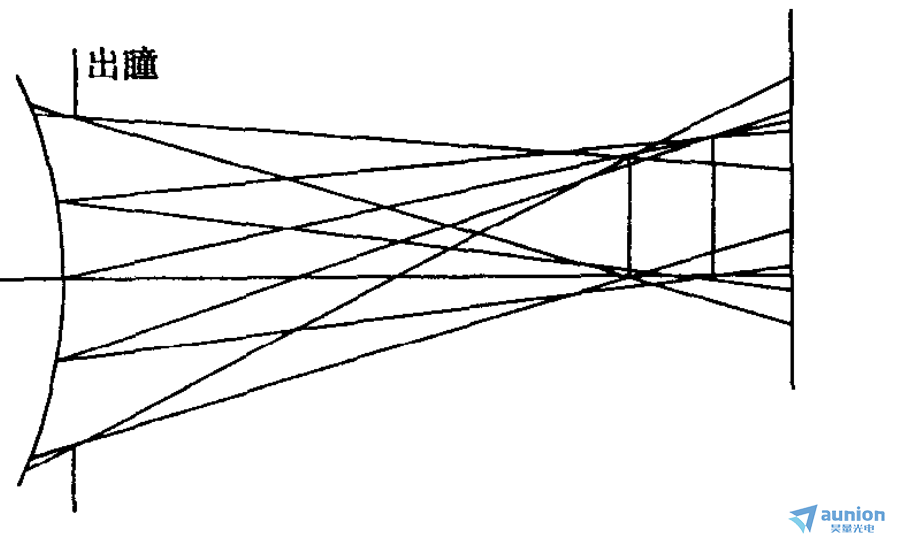
这时所要满足的条件称等晕条件(aplanatic condition)。即

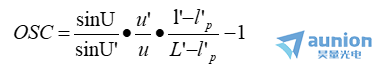
若OSC=0,表示系统满足等晕条件,OSC 称为正弦差。当轴上点由于球差而不完善成像时,满足此条件可使垂轴小面积等晕成像。
从以上公式可见,为计算正弦差以判断近轴点的像质,只需利用轴上点的光线计算结果,外加一条第二近轴光线的计算即可达到目的。为使正弦差的公式表示得更明确、简洁和便于计算,将l'=L-δL'代入,并且一般总取u=sinU,忽略高次小量(即取sin U'=u'和L’=l后,上述公式可化为
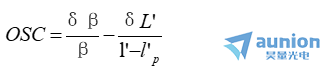
当物体位于无穷远时,按公式lsinU=h,可将上式表示成
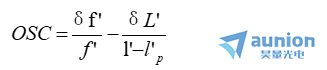
以上二式中,δβ和δf’分别由之前他们对应的表达式决定。
以上计算正弦差的公式中,都包含有出瞳位置因子l’p,它随孔径光阑位置而变。因此,当系统的球差已定而不满足等晕条件时,一定可以找到一个光阑位置使系统的正弦差为零。挑选光阑位置来校正某一种与其有关的像差是光学设计时常用手段。
相关文献:《几何光学 像差 光学设计》(第三版)——李晓彤 岑兆丰
您可以通过我们的官方网站了解更多的产品信息,或直接来电咨询4006-888-532。
展示全部 
展示全部 
