绝大多数实际光学系统的成像是不完善的，像差就是不完善之处的具体表述。像差的种类多，描述复杂，我们不仅仅要从像差的几何意义和表现特点入手，我们还要从像差的理论上深入研究，明确像差的表达式和计算。
像差理论与计算系列（五）慧差的计算
一、慧差
当光学系统不满足等晕条件时,轴外点成像将会产生彗差(coma）。由之前的像差概述技术文章中可知，彗差是一种描述轴外点光束关于主光线失对称的像差,应分别对子午光束和孤矢光束求取。
对于单个球面,彗差一方面是球差引起的,球差越大,彗差也会越大；另一方面,折射球面产生的彗差还与光阑位置、即主光线的入射角ip有关。如果光阑位于球心，相当于主光线与辅轴重合，即ip=0,则不论球差如何,都不会产生彗差。
实际上,光学系统的各种像差总同时存在,所以在计算彗差时，并不能像定义的那样，真正求出一对对称光线的交点相对于主光线的偏离，而是以这对光线与高斯像面交点高度的平均值与主光线交点高度之差来表征的。
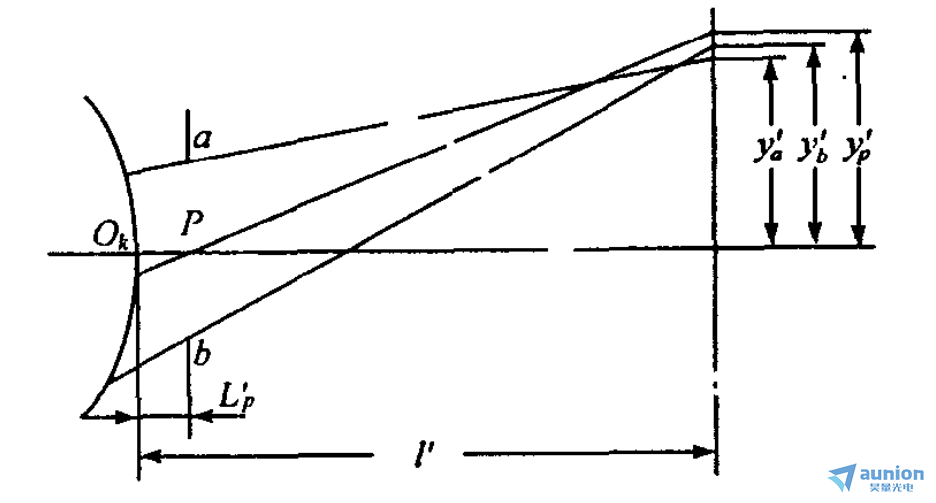
如上图所示,对于子午彗差，可表示为
对于弧矢彗差,因一对对称的弧矢光线与高斯像面的交点在y方向的坐标必相等，故有
彗差是轴外点成像时产生的一种宽光束像差，是与视场和孔径均有关系的。为全面了解光学系统对彗差的校正情况，需要计算设置多个特征视场和特征孔径来计算彗差。对于子午光束，孔径取点系数为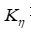
要正负都取，如±1，±0.85，±0.707，±0.5 和±0.3;对于弧矢光束，只对单向的光线计算即可，即
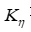只取正值。
如果光学系统不满足等晕条件，近轴轴外点就会产生彗差。所以彗差与等晕条件是有关系的。可以把近轴点的弧矢彗差归结为光学系统不满足等晕条件所导致的结果，由于视场很小时主光线与高斯像面的交点高度十分接近理想像高,可以证明这时有
大的彗差，严重影响轴外点的成像质量。所以说任何具有一定大小孔径的光学系统都必须很好地校正彗差。
实际像差与结构参数具有很复杂的关系,因此很难用显函数来表示彗差。讨论彗差现象有两种方法，一种是讨论初级彗差的现象，另一种是从折射球面的性质结合光的传播定性讨论彗差的现象。这里我们采用第二种方法。
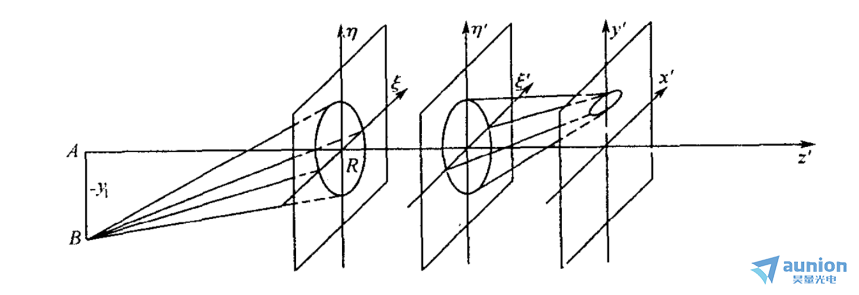
如上图，若假想在入瞳面上只有一中心在光轴上的细圆环透光,那么，由轴外点 B射出，能进人光学系统的光线构成了以B点为顶点的圆锥面光束。此光束经系统后，由于多种像差的影响，不再是对称于主光线的圆锥面光束，也不再会聚于一点，它与高斯像面相截成一封闭曲线，具有复杂的形状，但对称于子午平面。整个入瞳可看成由无数个不同半径的细圆环组成。由 B点发出过这些细圆环的光束，经系统后各自在高斯像面上截得大小不等、形状不一、并在 y’轴方向错开的封闭曲线，最后叠加成一个形状复杂的对称于子午平面的弥散斑。所以，当轴外点成像具有各种像差时，其像质是很差的，也难以得到各种像差对成像质量的影响。
因此,我们在讨论任何一种像差现象都必须把这种像差分离出来单独讨论，即认为当前的光学系统仅存在这一种像差。
由前面的讨论可知，当光学系统仅有彗差时,对于由出瞳出射的某一孔径带光线，其上下光线的交点在子午面内，但不在主光线上；前后光线相当于比主光线略高的一对光线，但没有上下光线那么高，它们的交点在辅轴上，但不在主光线上。这个孔径带上其他任何一对光线又相当于比前后光线孔径更大、但比上下光线孔径小的光线，它们的交点应该在前后光线的交点与上下光线的交点之间,但由于它们并不关于子午面对称。所以它们的交点不在子午面内。因此,由出瞳上各个直径方向的对应点出射的各对光线在像空间相交，把这些交点连起来以后将形成一个光环，光环最上方是子午光线的交点,最下方是弧矢光线的交点，其余各点对应其他的交点。孔径越大,像空间的这个光环也就越大，相应的交点离主光线就越远，于是形成了彗星形状的弥散斑。如下图所示。
对于单个折射球面,当主光线通过球心时满足等晕条件，不会产生彗差。这说明彗差与孔径光阑的位置有关。因此,如果一个光学系统存在残余球差，仍可找到某一个孔径光阑位置使系统能够校正彗差。慧差矫正在之前的技术文章中以及介绍过，此处不在重复介绍。
您可以通过我们的官方网站了解更多的产品信息，或直接来电咨询4006-888-532。
展示全部 
展示全部
