绝大多数实际光学系统的成像是不完善的，像差就是不完善之处的具体表述。像差的种类多，描述复杂，我们不仅仅要从像差的几何意义和表现特点入手，我们还要从像差的理论上深入研究，明确像差的表达式和计算。
像差理论与计算系列（七）畸变的计算
对于理想光学系统,一对共轭平面上的放大率是常数。但对于实际光学系统，只当视场较小时具有这一性质,而当视场较大或很大时，像的放大率就要随视场而异，这样就会使像相对于物体失去相似性。这种使像变形的缺陷称为畸变(distortion)。设某一视场的实际主光线与高斯像面的交点高度为yp’，当无彗差时，主光线即为成像光束的中心光线，因而yp’表征实际像高。它与理想像高y0’之差称为线畸变，即
常用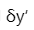 
相对于理想像高的百分比来表示嗬变，称相对畸变，即
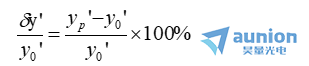
如果将实际放大率yp’/y记为β’,上述公式可以化为
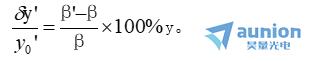
式中β为理想放大率。可见,实际放大率β’与理想放大率β之差与β之比即为该视场的相对畸变。对于大视场系统,与其他轴外像差一样,需对若千个视场计算畸变,然后以视场为纵坐标,畸变为横坐标画出畸变曲线。
有畸变或畸变很大的光学系统,若对等间距的同心圆物面成像,将得到非等间距的同圆。若物面为如下图(a)所示的正方形网格,我们可以很容易的分析得出，由正畸变的光学系统成的像呈枕形，如图（b)；由负畸变光学系统所成的像呈桶形，如图（c)。图中虚线所示是理想像。
可见，畸变仅由主光线的光路决定,它只引起像的变形，而对像的清晰度并无影响。因此,对于一般的光学系统，只要感觉不出它所成像的变形(相当于yp’/y0’≤4%，这种像差就无妨碍。但对某些要利用像来测定物体的大小和轮廊的光学系统，如计量仪器中的投影物镜、工具显微镜以及航空测量用的摄影物镜等，畸变就成为主要的缺陷了。它直接影响测量精度，必须严格校正。计量仪器中的物镜，畸变要求小于万分之几，但视场较小，矛盾并不突出;而航空测量用物镜视场大达 120 度，畸变要求小到十万分之几,校正就相当困难，导致镜头结构极度复杂。
值得指出,结构完全对称的光学系统以-1倍的倍率成像时，畸变能自然消除。这是因为实际放大率β’可写成
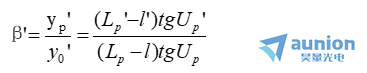
不管Up为何值，由于系统的结构对称于孔径光阑,B’恒等于-1而不会产生畸变。
对于单个薄透镜或薄透镜组，当光阑与之重合时，主光线通过主点，沿理想方向射出,与高斯像面的交点接近与理想像高相等，也不产生畸变，如下图（a）所示。以上双胶合物镜例子经计算足以说明这一结论。据此可以推知，当光阑位于透镜之前时，yp’小于理想像高y0’,产生负畸变,如如下图（b）;反之,当光阑位于透镜之后时产生正畸变。这表明了畸变对光阑位置的依赖关系。
相关文献：《几何光学 像差 光学设计》（第三版）——李晓彤 岑兆丰
您可以通过我们昊量光电的官方网站www.auniontech.com了解更多的产品信息，或直接来电咨询4006-888-532，我们将竭诚为您服务。
展示全部 
展示全部
